👀 계량경제학 개인 공부용 포스트 글입니다.
1. Motivation
① Motivation
• CMI 의 위배는 인과추론을 실패하게 만든다.
• 도구변수의 사용에 있어서도, zi 가 완전히 random assignment (ex. military lottery) 한 경우가 아니라면, cov(zi, v) = 0 을 의심할 많은 이유가 있을 수 있다. (xi = ϒ0 + ϒ1•zi + v)
• 인과추론의 golden rule = randomization = treatment 를 제외하고 treatment group 과 control group 은 Cetris Parbius 하다
• 사회과학 연구에서 RCT 는 윤리적인 이유, 비용문제, 사람을 대상으로 하는 실험은 고려할 부분이 많다는 점 (Hawthrone effect) 등의 이유로, 매우 까다로운 문제가 된다. 대신에, natural experiment 를 진행하는 경우가 많다.
② Natural experiment
• quasi-experiment (natural experiment) 는 관심변수 x에 대한 무작위 할당 (또는 변화) 를 유발하는 사건에 해당한다.
• 실험 상황에 노출된 개개인은, treatment 를 random 하게 받는다.
2. Simple differences
① DiD
• quasi-experiment (natural experiment) 를 진행한다고 했을 때, DiD estimator 방법을 사용하는 경우가 많다.
• Difference : treatment 가 random 하게 할당된다고 했을 때, treated group 에서의 결과 y 와 untreated group 에서의 결과 y를 비교한다.
• Difference in Difference : panel data 에서 cross-sectional 한 차이 뿐 아니라, time-series 적인 차이도 고려하는 방법을 말한다.
② Cross-Sectional Difference
• yi = β0 + β1•Di + ui ⇨ regression only contains post-treatment data
• Di = 1 : i 가 treatment group 에 속할 경우
• β1 이 causal 이 되기 위한 가정 ⇨ E(ui | Di) = 0 : treatment is uncorrelated with the error
↪ 즉, post-treatment 기간에서 y의 기대수준은, 개인이 treated 받았는지 아닌지와는 관련이 없음을 의미한다.
↪ 직관적으로 말하자면 selection bias 가 없다는 것을 의미한다!
• No selection bias : treatment 가 존재하지 않을 때, treated group 에서의 y의 기댓값은 control group 에서의 y 의 기댓값과 동일할 것이다. lab experiment 에서는 가능한 상황이지만, natural setting 에서는 비슷한 수준의 y를 갖는다고 가정하기 어렵다.
• 간단한 post-treatment difference 에서 처치그룹과 통제그룹에서의 selection bias 는 회귀 추정치를 편향시킬 수 있다. individual fixed effect 는 treatment 와 collinear 하기 때문에, 간단한 difference model 에서 individual FE 를 사용할 수는 없다.
③ Time-series
• yt = β0 + β1•Pt + ut
• treated group 이 treatment 를 받기 전과 후의 y에 대한 차이를 비교한다.
• 실험에 의해 처치받은 관측치들만 포함시킨 회귀식
• Pt : period t 에서 treatment 가 발생했다면 1, 아니면 0 의 값을 가짐
• β1 이 causal 이 되기 위한 가정 ⇨ E(ut | Pt) = 0 : treatment is uncorrelated with the error
↪ after treatment effect p , post-treatment 기간에서의 y의 기대수준은 pre-treatment 기간에서의 y의 기대 수준과 비슷할 것이다.
↪ treatment 가 없을 때, post-treatment 기간과 pre-treatment 기간에서의 평균적인 y 가 같을 것이라는 가정을 도입한다.
• simple pre- and post-difference model 에서, 처치그룹에서 time-varying trend 는 회귀 추정식을 편향시킬 수 있다. time FE 는 pre- and post-difference 에 collinear 하기 때문에 time FE 를 simple difference model 로 사용하기는 어렵다.
3. DiD
① Basics
• treated group 에 대한 사전 대 사후 처리(first difference) 의 변화와, untreated 그룹에 대한 사전 대 사후 처리(second difference)의 변화를 비교
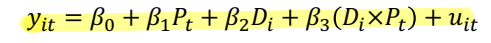
• β1 : treated group 과 untreated group 에서 공통적으로 보이는 사전처리 기간부터 사후처리 기간까지 평균적인 y 변화량 ⇨ common time trend
• β2 : 사전처리 기간과 사후처리 기간에서 공통적으로 보이는 treated group 과 untreated group 에서의 y 의 평균적인 차이 수준 ⇨ Group specific characteristic (difference b/t treated and untreated)
• β3 : 사전처리 기간부터 사후처리 기간동안 untreated group 에서의 y의 변화와 비교한 treated group 에서의 y의 평균적인 차이 변화량 (average differential change in y) ⇨ DiD estimate ⭐

② Visualization
• Data Viz

• β2 : treated 와 untreated group 간의 차이를 설명

• β1 : pre-treatment 와 post-treatment 간의 차이를 설명
⇨ β1 을 데이터에서 제거했을 때

⇨ β2 를 데이터에서 제거했을 때


⇨ 결과로 나온 β3 가 DiD estimate 를 설명하는 부분이 됨
③ Identification
◯ Parallel trends
• β3가 treatment 의 인과효과를 나타낼 때?

• non-parallel trends bias 가 0 이라는 가정이 필요하다. 즉, 인과효과를 밝히기 위해선 parallel trend 가정을 만족해야 한다.

treatment 가 없다고 가정했을 때 (y0), treated group 에서의 y의 변화량은 untreated gropu 에서의 y 변화량과 같다. 그러나 selection bias 와 같이 parallel trend 도 직접적으로 test 하는 것이 불가능하다. treatment 가 존재하지 않을 때 E(y0 | Treat, Post) 혹은 treated group 에서의 counterfactual post-treatment 결과를 관측할 수 없기 때문이다.
◯ Violation of Parallel trends
• 아래와 같이 Parallel trend 가정이 만족되지 않는다면, treated group 에서의 y의 변화량이 treatment 때문인지, 다른 group-specific trend 의 영향 때문인지 밝히는 것이 쉽지 않다.

• treatment 없이 treated group 에서의 counterfactual post-treatment outcome 을 관찰하는 것은 불가능하기 때문에 parallel trend 가정을 test 할 수 없다.
• 대신에 pre-treatment 기간에서의 parallel trend 를 검토한다. 사전처리 기간에 parallel trend 를 보인다면, 사후 기간에 만약 treatment 가 없다고 했을 때 해당 가정이 유효하다고 보는 관점이다. 이를 parallel pre-trends 라고 한다.
④ Generalized DiD
◯ Generalized DiD : DiD 모델에서, group mean 을 설명하는 대신에, individual and time fixed effects 를 추가한다.
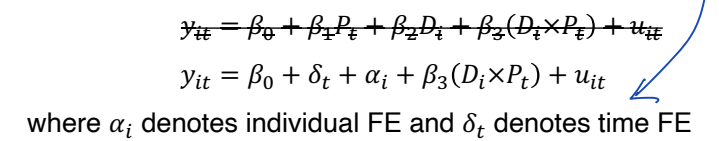
• Generalized DiD 의 장점은, precision 을 개선할 수 있고, model 의 설명력이 더 높아질 수 있다는 점이다.
• 처치집단과 통제집단 내에서 모든 개별 관측치들이 동일한 평균 y 를 가져야 한다는 가정이 필요하지 않는다. 개별 관측치들의 변동을 허락한다. 또한 시간에 따라 y의 일반적인 변화가 달라질 수 있다고 본다.
◯ Example

• time FE 는 actual trend 에 대해 설명한다.

⑤ Multiple events
• 다수 그룹의 관측치들에 대해 다수 시점에서 natural experiment 가 반복될 수 있다. 가령 미국의 50개 주에 대해 각기 다른 시점에 특정한 규제강화 조치를 적용할 수 있다.

• c : 다른 이벤트에 의해 treat 를 받은 개별 관측치들의 서로 다른 집합을 나타내는 인덱스 (코호트)
• β3 : 다수의 이벤트에 따른 평균적인 처치효과
• Pct = 0 : early periods for treated cohort with late treatment
• treated individual 의 특정 시점에서의 untreated 관측치는 control group 으로 볼 수 있다.
※ 코호트 : 특정 기간동안 공통된 특성이나 경험을 갖는 사용자 집단을 코호트라고 한다. 코호트 분석은 소비자들의 행동이 시간에 지남에 따라 어떻게 변하는지 그 추세에 대한 깊은 이해를 제공한다.
⑥ Event study
• Multiple event 에서 "pre-treatment" 에 대한 정의는 사라진다. 개별 관측치를 사전/사후 처리로 나누는 것 대신에, treatment 가 시작된 기간 이후의 추세에 대해 검토한다.

• t=0 일 때 treatment 가 발생되며, t_min 이 earliest year, t_max 가 latest year 에 해당
• βj : the difference in y between the treated and the untreated in period j relative to excluded period
• βj 의 신뢰구간 그래프를 그려봄으로써 differential trend 를 살펴볼 수 있다.

⑦ Falsification Tests
• parallel pre-trends 를 확인하는 것은 DiD 추정치의 타당성을 살펴보기 위한 falsification test 라 볼 수 있다.
• 방법 1 : pre-treatment 관측치 비교
↪ Idea : treatment 가 랜덤하게 배정되어, treatment 이전에 처치집단과 통제집단의 특성이 동일해진다.
↪ treated 관측치와 untreated 관측치가 y에 영향을 미치는 것으로 간주되는 차원에서 두 집단이 비슷하다는 것을 보여주면 할당이 무작위인지 확인하는데 도움이 될 수 있다.
• 방법 2 : treatment reversal
↪ 규제/법이 폐지되는 예시처럼, natural experiment 가 나중 시점에서 역전되는 경우가 발생할 수 있다. 역전이 반대 효과를 발생시킬 수 있다고 기대할 수 있다면 해당 효과를 확인해 보는 것도 좋은 방법이다.
• 방법 3 : Unaffected variables
↪ natual experiment 에 의해 영향을 받지 않는 변수임을 입증함으로써 treatment 효과만 밝혀낼 수 있다. (treatment 외에 다른 효과가 없다)
• 방법 4 : triple-difference
4. Triple differences
• 처치효과에 더 민감하거나 덜 민감한 관측치가 발견된다면, 이러한 heterogeneous 한 결과에 숨겨진 메커니즘을 밝히는 것이 중요하다

• DDD 는 treatment 와 control 을 비교하기 어려울 때 연구 디자인으로 채택할 수 있다.
↪ 예를들어 노인을 대상으로 한 의료 정책 변화의 효과에 대한 연구를 진행한다고 했을 때, treatment 집단을 65세 이상인 사람, control 집단을 55세~65세 사이인 사람으로 설정해 볼 수 있다. 만약 DiD 분석을 한다고 하면, 나이가 젋은 그룹과 나이든 그룹의 건강 결과 경로에 개입이 없는 경우 체계적으로 건강 수준이 다르지 않았을 것이라 가정한다. 그러나 65세 전후로 건강상태의 변화는 클 수 있다. 따라서 의료정책이 없는 다른 주에 거주하는 65세 이상인 사람들을 additional control 로 추가한다.

↪ β6 : DiD estimate for the less-sensitive observations : untreated group 에서의 less sensitive 관측치에 대한 y의 변화와 관련하여 treated group 의 less sensitive 관측치의 y 평균 차이 변화에 대해 설명한다
↪ β7 : how larger the treatment effect is for the more sensitive observations, how different the difference-in-difference estimate is for the more sensitive observations
↪ total effect for the sensitive group : β6 + β7
5. External validity
• 랜덤화는 internal validity 를 보장한다.
• External validity : 다른 setting 에 대해서도 적용할 수 있는가 : Can we extrapolate the finding to other settings?
↪ 기존과 비슷하다는 것을 보여 주어야 함
'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 강의_한치록_가정의 현실화 12장 (1) | 2023.05.22 |
|---|---|
| 계량경제학 강의_한치록_다중회귀 11장 (0) | 2023.05.21 |
| 계량경제학 강의_한치록_다중회귀 10장 (1) | 2023.05.19 |
| 계량경제학 강의_한치록_다중회귀 9장 (0) | 2023.05.18 |
| 계량경제학 스터디 Lecture 6. Panel Data (1) | 2023.05.16 |

댓글