👀 계량경제학 개인 공부용 포스트 글입니다.
1. Motivation
① Confounder
• 인과추론의 핵심은, 관측된 confounder 들을 control 하는 것으로, covariates 에 대해 condition 을 부여하거나, treatment 가 error 와 상관관계가 존재하지 않아야 한다.
• 그러나 대부분의 변수들은 본질적으로 관측될 수 없다. confounder 가 관측될 수 없는 경우, IV 를 사용해볼 수 있다. 그러나 좋은 도구변수는 찾기가 어렵다.
② Panel data
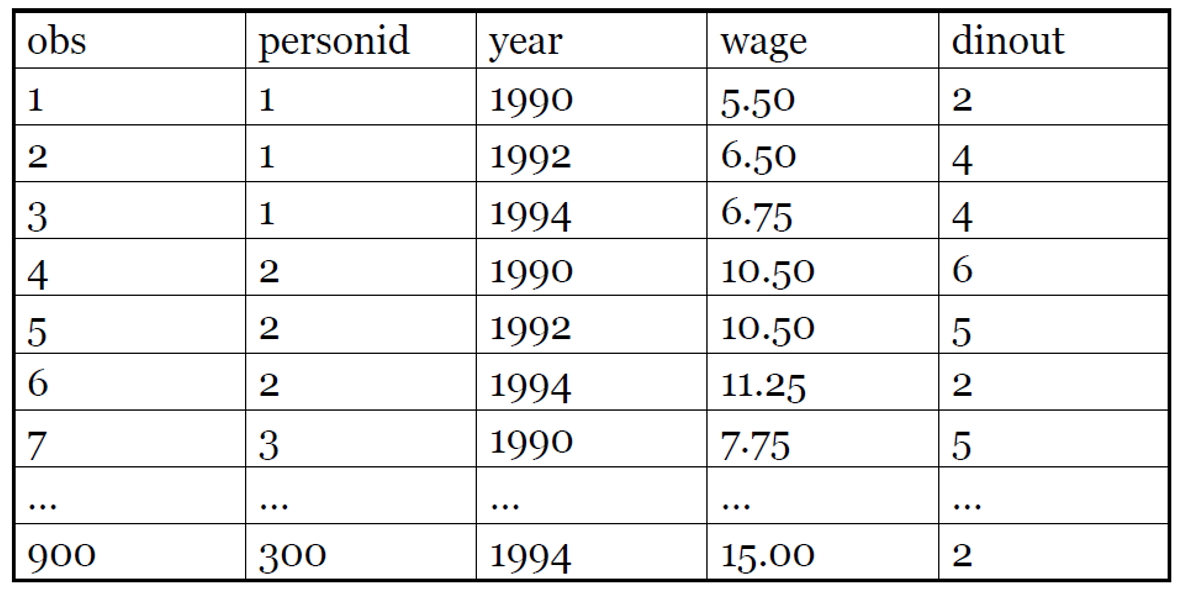
• 패널 데이터 구조에서, 관측될 수는 없지만 fixed 된 confounder 를 control 할 수 있는 추가적인 방법이 있다. 즉, 패널 데이터에서 time-invariant omitted 변수를 통해 문제를 해결할 수 있다.
• OV가 있을 경우 내생성 문제(endogeneity problem)가 있을 가능성이 높다. 여기서 패널 데이터의 특징을 이용하면 OV가 time invariant 할 때 OVB를 제거할 수 있다.
• Panel data : 여러 시간에 걸쳐 개인들에 대해 반복적으로 관측된 데이터 (repeated observations on individuals over time. Ex. 구매이력, 로그인 데이터)
• Balanced panel 데이터는 모든 i 에 대해 T 시점 관측치, N개 단위로 구성된다.
• Unbalanced panel 에서는 t가 일정하지 않는 경우가 많다. Entry,exit 시점이 다를 수 있고, 데이터 수집의 오류일 수도 있다.
2. Fixed effects model
① Fixed effects model
• fixed-effects 모델을 살펴보자
• fi : 관측되지 않은 time-invariant 한 변수 (confounders)

• corr(x_it, fi) ≠ 0 : f 를 control 하지 않으면 OVB 가 발생할 수 있다.

• 만약 fi 없이 모델을 추정하게 되면 x_it 는 v_it 와 상관관계가 발생하게 된다. (corr(x_it, fi) ≠ 0) 이는 CMI 를 위배하게 된다. 따라서 추정치에 bias 가 생긴다.
③ Within Transformation
• dependent variable 에 대해 평균을 취한다. (t에 대한 평균)

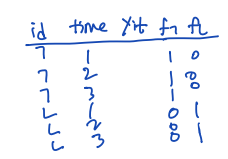
• 구한 yi_bar 를 yit 에서 뺀다. 그러면 fi 가 제거된다 (time-invariant 하기 때문)
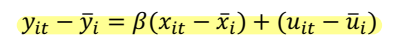
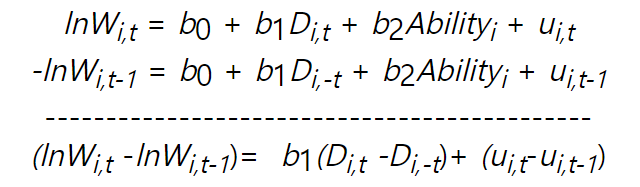
• (x_it - xbar) 와 (u_it - ubar) 가 uncorrelated 한 것은 exogeneity 가정에 의해 쉽게 보일 수 있다. 위와 같이 변형한 식에서 OLS estimation 을 진행하면 β 는 consistent 한 estimate 가 된다. 이러한 변형은, group (여기서 group 은 individual 한 사람을 말한다) 에 대해 모든 변수를 demeans 하기 때문에 'within transformation' 이라고 부른다.
• 패널 데이터 분석에서 분석 단위들은 각자 고유한 특성을 가지고 있다. (unobserved heterogeneity). 이러한 변수들은 predictor variable 에 영향을 미칠수도, 미치지 않을수도 있다. 그러나 데이터 수집과정에서 이러한 변수를 모두 수집하는 것은 불가능하다. 따라서 Fixed effect 모델을 사용한다. time-invariant 한 특성을 제거할 수 있어 다른 예측변수로 나타나는 순수한 time-variant effect 를 측정할 수 있다. 패널모델을 추론하는 방법은 크게 (1) LSDV, (2) Within Estimator, (3) First-Difference 가 있다.
④ Unobserved Heterogeneity
• Unobserved variable, fi 는 매우 흔하다. ex. 혀길이
• fi 는 fixed unobserved variables 들을 포함한다. ex. 혀길이, 귀길이, 손톱길이
• fi 는 오직 i 에 대한 unobserved variable 에 대해서만 포착한다. 따라서 각 개인별로 fi 는 다를 수 있다. 따라서 fi 를 "unobserved heterogeneity" 라고도 부른다. (개인마다 다른 눈에 보이지 않는 특성)
4. LSDV
Least squares dummy variables, LSDV
• 패널그룹의 특징을 이진 더미 변수로 처리하고 회귀분석을 진행하는 방식으로, n-1개의 더미변수를 포함시켜 효과를 파악한다. 추정해야 하는 파라미터가 많아, R-sqaured 값이 높을 수 밖에 없으며, 과적합이 이루어질 수 있기 때문에 패널 그룹의 수가 작고, 그룹 간 특성 차이가 중요한 경우에 사용한다. LSDV 와 달리, Fixed effect 모델은 더미변수를 사용하지 않고 within estimation 방식으로 개별 유닛의 그룹의 평균으로부터의 편차를 이용한다.
• fi 를 indicator variable 로 간주하고 아래와 같이 수식을 작성해 볼 수 있다. 각 group i 별로 dummy variable 을 만들어 회귀분석에 추가한다.
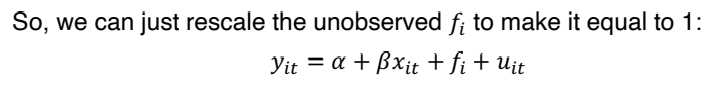
• n개의 entity 가 있을 때, 가령 패널 자료 안에 n명의 사람이 있을 때, 각 entity 를 나타내는 n-1 개의 더미변수를 만들고 이를 회귀식에 넣는다. 즉, 1번 더미변수는 사람1로 부터 나온 데이터면1, 아닌 다른 사람으로부터 나온 데이터면 0을 부여하고, 이런식으로 n-1 번 더미변수까지 쭉 만든 후 회귀식에 넣는다. 그러고나서 OLS 추정량을 구한다 ⇨ ui라는 개별 entity의 특성을 나타내는 오차항을 그냥 Di라는 더미변수로 바꾼것
5. Fixed effects model 장단점
① Benefits
• Omitted variable bias 로 인한 내생성 문제를 해결할 수 있다. 한 개인을 여러해에 관찰한 데이터를 이용하면 시간에 따라 변하지 않는 개인의 관찰불가능한 특성들을 통제할 수 있다. (Within estimator)
⑴ group i 에 있는 각 x 와 fi (each fixed effect) 사이의 correlation 을 허용한다.
⑵ 매우 직관적인 해석이 가능하다. cross-section 에서의 변화에 대해서만 회귀계수를 해석해 볼 수 있다.
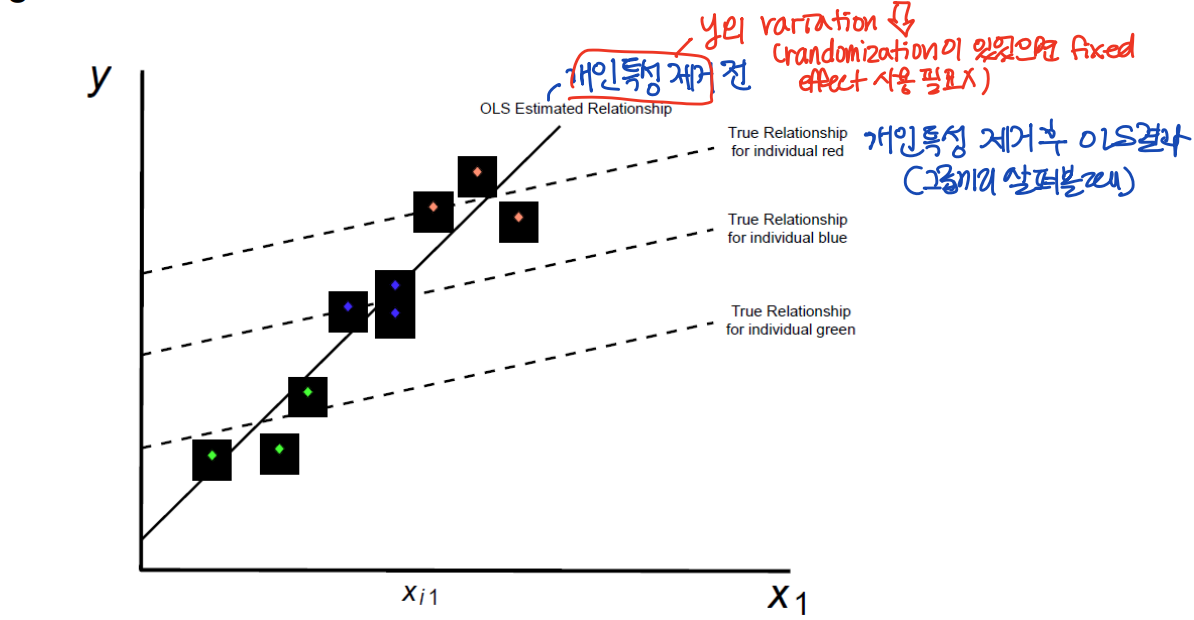
⑶ 관측되지 않은 이질성의 다양한 유형에 대해 유연하게 control 할 수 있다. Time FE 는 시간 흐름에 따른 관측되지 않은 이질성에 대해 설명한다.
※ 관측치들은 잠재적인 confounder 에 따라 grouped 될 수 있다.
② Costs
⑴ Can’t identify variables that don’t vary within group
group 내에서 변하지 않는 변수는 식별 할 수 없다. 독립변수 x에 대해 within-group variation 이 없다면, group FE 로부터 풀 수 없다. 만약 x가 group FE 에서 collinear 하다면, within transformation 에서 제거될 것이다.
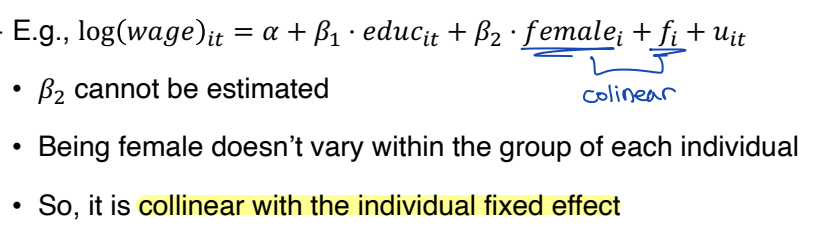
또한 X의 지속적인 변화가 Y에 반응할 수 있는 경우에도 문제가 될 수 있다. 이때 FE 를 추가하면, 관련 변수가 사라질 수 있다.
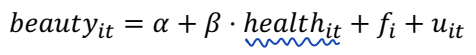
FE 를 사용하면 일시적인 변화만 남게 된다. 그러나 beauty 를 설명하는 가장 중요한 변이는 DNA 이다. 즉, X의 sustained component 가 y 의 중요한 결정 요인이 될 수 있다.
⑵ Subject to potentially large measurement error bias
독립변수의 measurement error 가 증폭될 수 있다. FE 를 추가하면 좋은 variation 부분이 제거될 수 있다.
⑶ Can be hard to estimate in some cases
하나 이상의 FE 유형을 사용하고, 데이터가 클 때 (N, T 모두 클때), 회귀분석에서 dummy variable 의 숫자가 증가할 수 있다.
⑷ Incidental parameter problem (optional)
샘플 크기가 증가할 때 (more individuals) 추정해야 될 파라미터 개수도 더 증가한다. 이때 FE 모델은 inconsistent 해질 수 있다.
또한 nonlinear panel data 에 대해서도 FE 로는 추정이 불가능하다. Logit, Tobit, Probit 모델을 사용해야 한다.
6. First Differencing (FD)
① FD
• 관측 불가능한 이질성을 제거하는 또 다른 방법이다. 각 변수에서 변수의 그룹 평균을 빼는 대신, 변수에서 지연된 관측값을 뺀다. (subtract lagged observatoin)
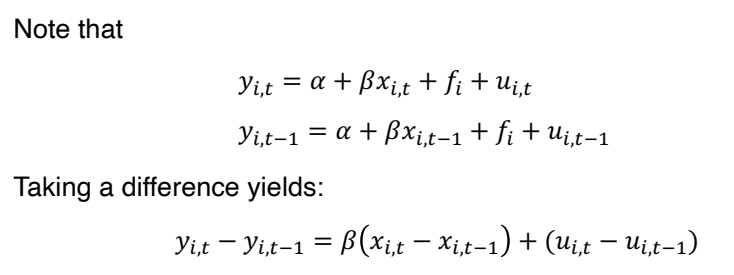
• 외생성 가정 (x_it, u_is 가 모든 t와 s에 대해 uncorrelated 하다) 이 만족된다면, β 는 consistent 하다.
② FD vs FE
• FD 와 FE 결과는 동일하다. 차이점은 efficiency 로, FE 는 u_it (disturbances 교란) 가 serially uncorrelated 할 때 보다 효율적이고, FD 는 u_it 가 random walk 를 따를 때 보다 효율적이다.
7. Stock and Watson Example
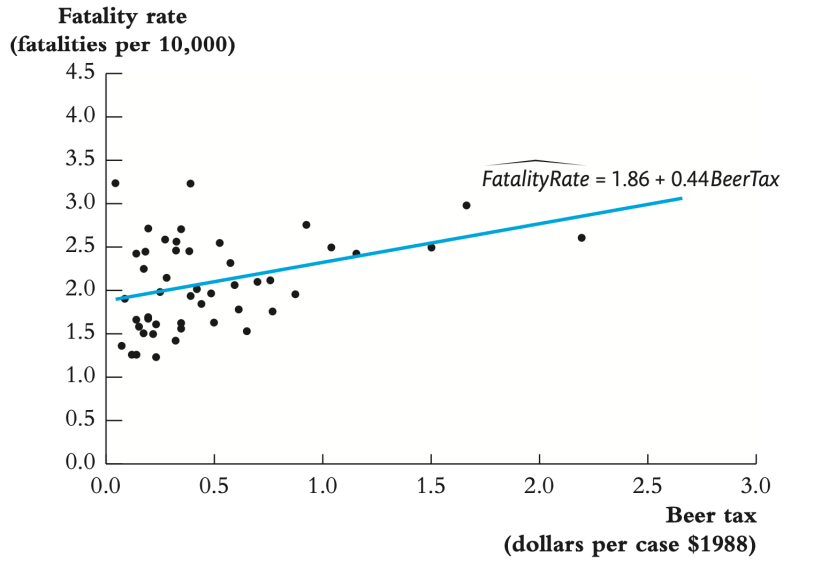
• 주류세를 높이면 사망률이 증가한다는 결과로, 직관적으로 알고있는 결과와 다르다 → 내생성이 있기 때문이라 볼 수 있음
• Potential OVB : state 별로 다르지만, 시간에 따라서는 상수값을 가짐
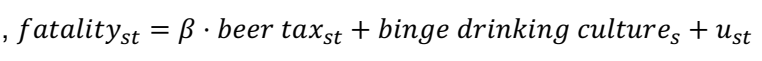
↪ binge drinking culture: Culture of drinking : 폭음 문화가 있는 주에서는 주류세가 높고 사망률이 높을 수 있다.
↪ 회귀분석에 FE 를 적용하지 않으면 bias 가 발생한다.
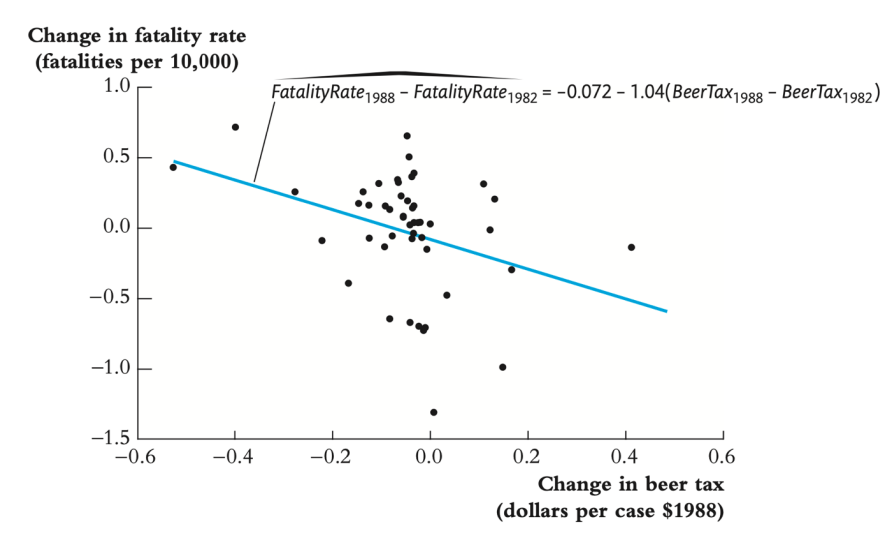
• state FE 를 포함하면, time-invariant unobserved heterogeneity 와 연관된 OVB 를 제외시킨다.

8. Lagged Dependent Model with FE
• lagged 된 종속변수와 관찰되지 않은 FE 를 모두 가진 모델의 경우 쉽게 추정할 수 없다.
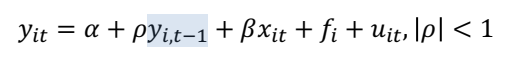
• x_it 와 fi 가 uncorrelated 되어있더라도 FE 를 무시하여 추정할 수가 없다.

9. Practical Tips, RE model
• Stata 같은 프로그램에서 FE estimator 를 사용하면 자동으로 within transformation 을 진행해준다.
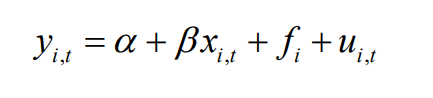
• Random Effect model 은 FE 와 매우 비슷하지만, fi 와 x가 uncorrelated 되어있다는 가정에서 차이가 있다.
• Fixed effect model 은 개별 단위의 특성을 포함하여 인과 관계를 추정한다. 반면, Random effect model 은 개별 단위 간의 변동성을 임의로 처리하는 방법이다. 개별 단위 간의 변동성을 랜덤 효과로 취급하여 모델에 포함한다.
'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 강의_한치록_다중회귀 10장 (1) | 2023.05.19 |
|---|---|
| 계량경제학 강의_한치록_다중회귀 9장 (0) | 2023.05.18 |
| 계량경제학 강의_한치록_다중회귀 8장 (0) | 2023.05.16 |
| 계량경제학 스터디 Lecture 5. Instrumental variables (0) | 2023.05.15 |
| 계량경제학 강의_한치록_단순회귀 7장 (0) | 2023.05.15 |

댓글