📌 아래 블로그의 코드와 Pytorch Geometric 라이브러리 설명을 참고해 공부했습니다.
https://baeseongsu.github.io/posts/pytorch-geometric-introduction/
예제를 통해 알아보는 PyTorch Geometric 5 Basic Concepts
다음 글은 PyTorch Geometric 라이브러리 설명서에 있는 Introduction by Example 를 참고하여 작성했습니다.
baeseongsu.github.io
https://pytorch-geometric.readthedocs.io/en/latest/notes/introduction.html#
Introduction by Example — pytorch_geometric documentation
We shortly introduce the fundamental concepts of PyG through self-contained examples. At its core, PyG provides the following main features: PyG contains a large number of common benchmark datasets, e.g., all Planetoid datasets (Cora, Citeseer, Pubmed), al
pytorch-geometric.readthedocs.io
1️⃣ Data Handling of Graphs
🔹 그래프
• Node 와 이를 연결하는 Edge 를 하나로 모은 자료구조
• G = (V,E)
🔹 Pytorch Geometric
• 하나의 그래프 → torch_geometric.data.Data 라는 클래스로 표현
• 속성
| data.x | • 노드 특징 행렬 • [num_nodes, num_node_features] |
| data.edge_index | • 그래프의 연결성 • [2, num_edges] |
| data.edge_attr | • 엣지 특징 행렬 • [num_deges, num_edge_features] |
| data.y | • 학습하고 싶은 대상 (target) • 그래프 레벨 → [num_nodes, *] • 노드 레벨 → [1, *] |
| data.pos | • 노드 위치 행렬 • [num_nodes, num_dimensions] |
→ 위의 속성들은 옵션으로 구성하고 싶은 속성을 선택해 다양하게 모델링이 가능하다.
① 그래프 데이터 생성 코드 예시
import torch
from torch_geometric.data import Data
edge_index = torch.tensor([[0,1,1,2],
[1,0,2,1]], dtype = torch.long) # (2,4) 크기의 행렬 : 4개의 엣지
x = torch.tensor([[-1],[0],[1]], dtype = torch.float) # (3,1) 크기의 행렬 : 3개의 노드
data = Data(x=x, edge_index = edge_index)

∘ edge_index : (2,4) 크기의 행렬 → 4개의 엣지들 (양방향 그래프)
∘ x : (3,1) 크기의 행렬 → 3개의 노드와 각 노드는 단일값을 가짐

② 그래프 데이터 생성 코드 예시 : 엣지를 노드의 순서쌍으로 나타낸 경우
- (v1, v2) 와 같은 자료형 구조 형태로 입력할 경우 contiguous() 를 사용해 표현한다.
# 엣지를 노드의 순서쌍으로 표현한 경우
edge_index = torch.tensor([[0,1],
[1,0],
[1,2],
[2,1]], dtype = torch.long)
x = torch.tensor([[-1],[0],[1]], dtype = torch.float)
data = Data(x=x, edge_index = edge_index.t().contiguous()) # 💡

• 함수
| data.keys | • 해당 속성 이름 |
| data.num_nodes | • 노드의 총 개수 |
| data.num_edges | • 엣지의 총 개수 |
| data.contains_isolated_nodes() | • 고립 노드 여부 확인 |
| data.contains_self_loops() | • 셀프 루프 포함 여부 확인 |
| data.is_directed() | • 그래프의 방향성 여부 확인 |
# 함수
print(data.keys) # 해당 속성 이름
👉 ['edge_index', 'x']
print(data['x']) # 노드 값
👉 tensor([[-1.],
[ 0.],
[ 1.]])
for key, item in data :
print(f'{key} found in data')
print(f'{item} found in data')
print()
👉 결과
x found in data
tensor([[-1.],
[ 0.],
[ 1.]]) found in data
edge_index found in data
tensor([[0, 1, 1, 2],
[1, 0, 2, 1]]) found in data
'edge_attr' in data # 엣지 특징 행렬이 있냐 - 없다.
👉 False
data.num_nodes # 노드의 개수
👉 3
data.num_edges # 엣지의 개수
👉 4
data.num_node_features # 노드 특성의 개수
👉 1
data.has_isolated_nodes() # 고립 노드 있는지 여부
👉 False
data.has_self_loops() # 자기 자신으로 화살표가 돌아오는 노드가 있는지 여부
👉 False
data.is_directed() # 단방향 그래프인지 여부
👉 False
# Transfer data object to GPU.
device = torch.device('cuda')
data = data.to(device) # GPU 사용으로 변경
2️⃣ Common Benchmark Datasets
🔹 데이터셋
• PyTorch Geometric 은 다양한 공통 벤치마크 데이터셋을 포함한다.
• 각 데이터셋마다 그래프 데이터 속성이 달라, 사용되는 함수가 다를 수 있다.
https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html
torch_geometric.datasets — pytorch_geometric documentation
category (string) – The category of the images (one of "Aeroplane", "Bicycle", "Bird", "Boat", "Bottle", "Bus", "Car", "Cat", "Chair", "Diningtable", "Dog", "Horse", "Motorbike", "Person", "Pottedplant", "Sheep", "Sofa", "Train", "TVMonitor")
pytorch-geometric.readthedocs.io
→ 데이터 목록
🔹 ENZYMES 데이터셋 예제
• 효소 데이터베이스에서 얻은 600개의 단백질 3차 구조 데이터셋 : 효소의 명명법과 관련된 정보가 저장되어 있다.
• 6개의 효소에 관련된 데이터가 포함되어 있다.
from torch_geometric.datasets import TUDataset
dataset = TUDataset(root = '/tmp/ENZYMES', name = 'ENZYMES')
dataset
print(len(dataset)) # 그래프 개수
print(dataset.num_classes) # 그래프 클래스 수
print(dataset.num_node_features) # 노드의 특징 수
600
6
3
→ 6종류의 클래스를 가진 600개의 그래프
• 인덱스 슬라이싱을 통해 데이터 확인
data = dataset[0] # 인덱스 슬라이싱을 통해 데이터 확인하기
print(data)
👉 결과
Data(edge_index=[2, 168], x=[37, 3], y=[1])
# edge_index=[2, 168] : 84 개의 엣지 (2 : 양방향, 엣지 개수 : 84개)
# x=[37, 3] : 37개의 노드와 3개의 노드 특성 (하나의 노드가 3개의 값을 가짐)
# y=[1] : 그래프 레벨 타겟
∘ edge_index=[2, 168] : 84 개의 엣지 (2 : 양방향, 엣지 개수 : 84개)
∘ x=[37, 3] : 37개의 노드와 3개의 노드 특성 (하나의 노드가 3개의 값을 가짐)
∘ y=[1] : 그래프 레벨 타겟
data.is_undirected() # 양방향 그래프인가요 - 네
True
train_dataset = dataset[:540]
test_dataset = dataset[540:]
print(train_dataset)
print(test_dataset)
👉 결과
ENZYMES(540)
ENZYMES(60)
dataset = dataset.shuffle() # 데이터셋 셔플
print(dataset)
👉 결과
ENZYMES(600)
🔹 Cora 데이터셋 예제
• 2708 개의 과학 논문들로 구성된 데이터셋
• 논문은 다른 논문들을 인용하기도 하는데, 이 연결구조를 표현한 것이 바로 Citation Network 이다.

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root = 'tmp/Cora', name = 'Cora')
print(len(dataset)) # 데이터셋 전체가 하나의 그래프임
1
print(dataset.num_classes) # 7개의 클래스
7
print(dataset.num_node_features) # 1433개의 노드 특성 (하나의 노드에 1433개의 값이 존재)
1433
∘ 데이터셋 전체가 하나의 그래프이고, 7개의 노드 클래스가 존재하며, 하나의 노드에 1433개의 값이 저장되어 있는 구조
data = dataset[0]
data
👉 결과
Data(x=[2708, 1433], edge_index=[2, 10556], y=[2708], train_mask=[2708], val_mask=[2708], test_mask=[2708])
∘ edge_index=[2, 10556] : 5,278 개의 엣지 (2 : 양방향, 엣지 개수 : 5,278개)
∘ x=[2708, 1433] : 2708개의 노드와 1433개의 노드 특성 (하나의 노드가 1433개의 값을 가짐)
∘ y=[2708] : 그래프 레벨 타겟
print(data.is_undirected()) # 양방향 그래프
True
data.train_mask.sum().item() # 학습하기 위해 사용하는 노드
140
data.val_mask.sum().item() # 검증 시 사용하는 노드
500
data.test_mask.sum().item() # 테스트 시 사용하는 노드
1000
3️⃣ Mini-batches
🔹 배치 단위의 학습
• PyTorch Geometric 은 sparse block diagonal adjacency matrices 를 통해 미니배치 형태로 만들고, 병렬화처리를 수행한다.
• feature 행렬과 target 행렬도 노드 기준으로 동일한 형태로 구성해야 한다.
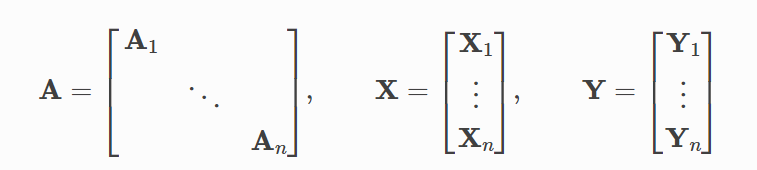
• torch_geometric.data.DataLoader 를 통해 배치 단위로 데이터를 처리
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
dataset = TUDataset(root = '/tmp/ENZYMES', name = 'ENZYMES',use_node_attr=True)
loader = DataLoader(dataset, batch_size = 32, shuffle = True) # ⭐
for batch in loader :
print(batch)
print(batch.num_graphs)
...
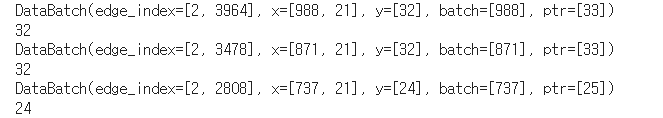
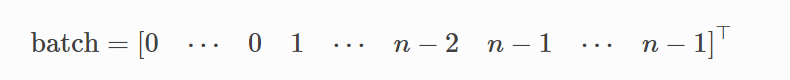
• batch = [984] : 984 개의 노드에 대해 32개의 배치를 부여
4️⃣ Data Transforms
🔹 데이터 변환
• torch_geometric.transforms 로 데이터 변환을 손쉽게 할 수 있다.
• torch_geometric.transforms.Compose 를 통해 다양한 변환함수들을 손쉽게 구성할 수 있다.
🔹 ShapeNet dataset 에 데이터 변환을 적용한 예제
• 17,000 건의 3D 형태의 점 구름 (point clouds) 데이터를 포함하고 있으며 총 16개의 카테고리로 구성되어 있다.

from torch_geometric.datasets import ShapeNet
dataset = ShapeNet(root = '/tmp/ShapeNet', categories = ['Airplane'])
dataset[0]
👉 결과
Data(x=[2518, 3], y=[2518], pos=[2518, 3], category=[1])
∘ pos = [2518, 3] : 2518 개의 점 데이터와 3차원
∘ edge_index 가 없음 → 연결관계가 없는 데이터
import torch_geometric.transforms as T
from torch_geometric.datasets import ShapeNet
# 그래프 변환
dataset = ShapeNet(root = '/tmp/ShapeNet', categories = ['Airplane'],
pre_transform = T.KNNGraph(k=6),
transform = T.RandomTranslate(0.01))
∘ pre_transform = T.KNNGraph(k=6) : KNN 으로 데이터를 그래프 형태로 변환한다. 아래의 출력 결과를 보면 edge_index 가 추가된 것을 볼 수 있다. (연결상태가 생성됨)
∘ transform = T.RandomTranslate(0.01) : 각 노드의 위치를 조금 이동시킨다.
dataset[0]
👉 결과
Data(x=[2518, 3], y=[2518], pos=[2518, 3], category=[1])
5️⃣ Learning Methods on Graphs
🔹 그래프로 학습하기
• 그래프 데이터 핸들링, dataloader 생성, transforms 를 통해 데이터 변환 👉 이제 그래프를 학습시켜보자
🔹 GCN layer 를 구성하여 Cora 데이터셋에 적용하는 예제
• Task : Graph node classification (노드 분류 문제) : 논문 내 등장한 단어들과 인용 관계만을 통하여 어떤 종류의 논문인지 맞히는 문제
(1) 데이터 다운로드
from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/tmp/Cora', name='Cora')
• Citation Network 👉 Node = 논문 , Edge = 인용관계
• 논문에서 등장하는 1433개의 특정 단어를 모아 단어 사전으로 만들고, 논문마다 단어들의 등장 여부를 feature vector 로 만들어 노드의 특징을 만들어준다.
(2) GNN 생성하기
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
class Net(torch.nn.Module) :
def __init__(self) :
super(Net, self).__init__()
self.conv1 = GCNConv(dataset.num_node_features, 16)
self.conv2 = GCNConv(16, dataset.num_classes)
# 2개의 GCNConv layer
def forward(self, data) :
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training = self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
(3) 학습하기
# GPU 설정
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
# 옵티마이저 생성
optimizer = torch.optim.Adam(model.parameters(), lr = 0.01, weight_decay = 5e-4)
# 훈련
model.train() # 학습 준비
for epoch in range(200) :
optimizer.zero_grad() # 파라미터 초기화
out = model(data) # 예측값
loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask]) # 손실함수 계산
loss.backward() # 역전파
optimizer.step() # 파라미터 업데이터
(3) 테스트 데이터로 모델 평가
# 모델 평가
model.eval()
_, pred = model(data).max(dim=1)
correct = float (pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print('정확도 : {:.4f}'.format(acc))
https://colab.research.google.com/drive/1HDtOE5sZUPvA93ZT-OzXHuGgrSeU7hNk?usp=sharing
1주차 복습과제.ipynb
Colaboratory notebook
colab.research.google.com
'1️⃣ AI•DS > 📘 GNN' 카테고리의 다른 글
| [CS224W] Graph Neural Network (0) | 2022.11.24 |
|---|---|
| [CS224W] Message Passing and Node classification (0) | 2022.11.17 |
| [CS224W] PageRank (0) | 2022.11.02 |
| [CS224W] 1강 Machine Learning With Graphs (0) | 2022.10.11 |
| [CS224W] NetworkX , pytorch geometric Tutorial (2) | 2022.10.07 |



댓글