🐳 Mathematical Statistics with application 교재를 공부한 내용을 정리하였습니다.
Probability
1️⃣ Introduction
🔹 확률이란
▢ 미래의 사건 발생에 대한 신념
▢ Random events cannot be predicted with certainty, BUT the relative frequency with which they occur in a long series of trials is often remarkably stable 👉 장기적 상대도수 확률 : 실제 경험이나 실험을 통해 결과를 도출하는 확률

▢ 통계적 확률 : 실험에서 발생하는 결과는 표본이고, 실험을 무한히 반복하는 것은 표본이 모집단이 된다는 의미이며, 상대도수의 극한은 특정 확률 값에 수렴하기 때문에 많은 표본으로 모집단의 특성을 파악할 수 있다.
- Relative frequency : 반복시행 실험에서 시행 횟수에 대한 성공 횟수의 비율 = m/N
- 시행 횟수가 커짐에 따라 상대적 빈도수와 이론적 확률은 매우 가까워진다.
- 확률 = 시행의 횟수가 무한히 커질 때 어떤 사상의 상대적 빈도수의 극한치로 정의
2️⃣ Probability and Inference

🔹 확률과 통계적 추론
▢ 통계적 추론 : 관측된 표본들로부터 모집단의 통계적 특성 (확률분포함수, 확률밀도함수, 모수 등) 을 과학적으로 이끌어내어 모집단에 대해 추론하는 것
▢ 확률적 이론들은 통계적 추론의 근간이 된다.
▢ 확률 : 동일한 조건 하에서 동일한 실험을 무수히 많이 반복하여 실시할 때, 어떤 특정 사건이 발생하는 비율을 말한다. 나올 수 있는 모든 경우의 수 (표본공간) 중 어떤 특정한 조건을 만족하는 사건이 발생하는 비율
3️⃣ Set Notation
🔹 집합

▢ Universal set 전사건, empty set 공사건

▢ Subset, Union 합사건, Intersection 곱사건, Complement 여사건




▢ 배반사건 Mutually Exclusive (disjoint)

▢ 분배법칙

▢ 드모르간 법칙

4️⃣ Discrete Probabilistic
🔹 Experiment

▢ 많은 관측 값 중 하나의 결과를 산출하는 과정
EX. 동전 던지기
🔹 Events

▢ Event : 표본(샘플) 공간의 부분집합으로 어떤 조건을 만족하는 특정한 표본점들의 집합을 말한다.
👀 표본점 : 표본을 이루는 여러 원소를 각각 하나의 점으로 대응한 표본 공간의 점
▢ Simple events 단순 사상 : 실험 결과에서 오직 하나만을 포함하는 사건. 표본점 하나로 이루어진 사상
→ EX. B={4} 주사위의 눈이 4인 경우

▢ Compound events 복합 사상 : 하나 이상의 사건들의 집합. 여러개의 표본점으로 이루어진 사상
→ EX. A={2,4,6} 주사위의 눈이 짝수인 경우
🔹 Sample space
▢ Sample Space : 시행(Experiment)의 모든 가능한 결과의 집합



🔹 Discrete Sample space 이산형 표본공간

▢ 유한하고 셀 수 있는 숫자로 이루어진 표본점으로 이루어진 표본 공간

▢ 주사위를 던지고 1을 관측했다면, 동시에 숫자 2는 관측할 수 없다. 즉, E1 과 E2 의 사상은 서로 상호배타적인 관계에 있다. 이처럼 구분되는 simple events 들은 서로 상호배타적인 관계를 가진다.
▢ Compound events → collection of sample points

- A : 홀수가 나오는 경우
- B : 5보다 작은 숫자가 나오는 경우

→ discrete sample space S 에서 관측할 수 있는 event 는 표본점의 집합이다.
▢ 확률 모델 - 각 simple event 에 대해 수치적인 확률 값을 할당하는 것 - 상대도수 확률의 개념을 도입
🔹 공리적 확률
▢ 상대도수의 극한을 확률로 정의하는 것과 같이 실제 사용에서는 근사값을 이용하게 되는 빈틈이 있다. 고전적 확률이나 통계적 확률을 기반으로 하여 현대의 공리적 접근 방식이 제안되었다.
▢ 확률은 다음의 세 가지 공리 (axiom) 를 만족하는 집합 함수이다.

확률 P 는 S 의 부분집합들의 모임을 정의 구역으로 하고, 공리1,2,3 을 만족하는 실수값을 갖는 집합함수이다. 고전적 & 통계적 확률은 모두 위의 세 가지 공리를 만족한다.
5️⃣ Calculating the probability of an Event : The sample - point method
▢ 사건이 일어날 확률을 구하는 방법 : Sample point method vs Event-composition method
→ 이 챕터에서는 sample point 방법에 대해 알아볼 예정
🔹 sample point method

1. 실험에 속한 표본점의 속성을 정의
2. 표본 공간에 속하는 모든 표본점을 구하기
3. 구한 표본점들 각각에 대한 확률을 부여
4. 구하고자 하는 사건 정의
5. 사건에 속한 모든 표본점들의 확률을 더함
→ 이 방법은 표본 공간에 속한 표본점들이 많다면, 직접 구하기 힘들고 구하는 과정에서 실수가 많이 발생할 수 있다. 따라서 표본점을 세는 방법으로 수학적인 방법인 순열이나 조합을 응용할 수 있다.
6️⃣ Counting sample points
▢ 경우의 수를 구하는 방법들
🔹 mn rule

▢ 주사위를 두 번 던진다하면 처음 던질때 6가지 경우의 수, 두번째 던질 때 6가지 경우의 수로 총 36가지 경우의 수가 존재한다.
🔹 순열

▢ Ordered arrangement of r distinct objects : 표본 공간에서 원소를 뽑아 나열할 때 나타나는 경우의 수
🔹 모집단을 부분 집단으로 나누기

▢ The number of subset of various sizes
🔹 조합

▢ 표본점들의 순서를 생각하지 않는다.
7️⃣ Conditional Probability and Independence of Events
🔹 조건부 확률

▢ 어떤 사건(정보) 가 주어졌을 때 관찰되는 사건이 일어날 확률
🔹 독립

▢ 위와같은 수식을 만족할 때, 두 사건 A 와 B 는 독립관계에 있다고 할 수 있다.
▢ 독립 : 사건 A 가 사건 B 에 영향을 미치지 않는다는 뜻
8️⃣ Two Laws of Probability
🔹 곱셈법칙

▢ 조건부 확률을 이용하여 A와 B 사건의 교집합을 구하는 방법

▢ 조건부 확률을 이용하여 A와 B 사건의 교집합을 구하는 방법

▢ 조건부 확률 계산 일반화

🔹 덧셈법칙

▢ A 사건과 B 사건의 합집합을 구하는 공식

🔹 여집합의 확률을 구하는 법

9️⃣ Calculating the probability of an Event : The Event - Composition method
🔹 Event - composition method

▢ 합집합, 교집합 등으로 확률을 표현하는 방법

▢ Example

🔟 The law of total probability and Bayes' rule
🔹 전체 확률의 법칙

▢ 분할 : partition


▢ Bi 가 S 의 partition 일 때, P(A|Bi)*P(Bi) = P(A⊓B) 이다. 즉 S 의 분할인 모든 B 와 A 의 교집합을 구하고 그 교집합들의 확률을 더하면 A 의 확률이 된다.
🔹 Bayes Rule

- 앞서 설명한 전체확률의 정리를 이용해 증명 : Bk 는 S 의 partition 분할 이다.
머신러닝과 베이즈 정리
💡 머신러닝 알고리즘 나이브 베이즈 : Gaussian Naive Bayes , Multinomial Naive Bayes , Bernoulli native bayes
- 베이즈 결정이론 : 이진분류, 멀티클래스 분류
💡 베이즈 정리 : 새로운 사건의 확률을 계산하기 전에 이미 일어난 사건을 고려하는 것을 전제로 하는 베이즈 (혹은 베이지안) 통계의 근간
👀 농어와 연어의 분류 문제
⭐ P(Wi | x) = Posterior 사후확률
- x = 물고기의 피부밝기
- Wi : W1 = 농어, W2 = 연어
- 물고기의 피부밝기가 주어졌을 때 그 물고기가 클래스 wi 에 속할 확률
▢ P(wi | x) 는 바로 알기 어렵지만, P(x | wi) 는 관찰을 통해 쉽게 알 수 있다.
- 농어를 충분히 많이 잡아 어떤 피부밝기를 가진 농어들이 많은지에 대한 분포 구하기

⭐ P(x | wi) = likelihood 가능도
- 위와 같은 likelihood 그래프를 가지고 두 그래프가 만나는 접점을 기준으로 이하는 연어, 이상은 농어로 분류할 수 있을 것이다.
- 그러나 likelihood 만으로 분류를 하기 위해서는 연어와 농어가 같은 비율로 바다에 살고있다는 가정이 있어야 한다.
- 따라서 likelihood 만으로 posterior 를 바로 알기 어렵다.
- 특정 x 에 대해 연어의 가능도가 농어의 가능도보다 크다 하더라도 연어가 애초에 매우 희귀하게 발견된다면 물고기가 농어일 가능성도 생각해봐야하기 때문이다.
- 따라서 우리는 사전확률 Prior 즉, 농어가 잡힐 확률 P(w1) 과 연어가 잡힐 확률 P(w2) 를 알아야 한다.
⭐ P(wi) = Prior 사전확률
- 우리가 가지고 있는 사전 지식에 해당한다.
✅ Posterior P(wi | x) : 단서가 주어졌을 때 대상이 특정 클래스에 속할 확률로 우리가 최종적으로 구해야 하는 값
✅ Likelihood P(x | wi) : 각 클래스에서 우리가 활용할 단서가 어떤 형태로 분포되어 있는지 알려주는 값
✅ Prior P(wi) : 사전 정보로 주어지거나 주어지지 않으면 연구자의 사전 지식을 통해 정해주어야 하는 값


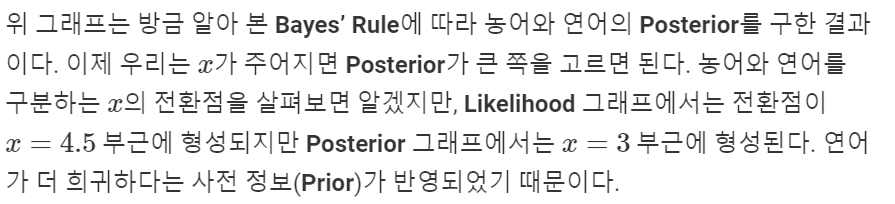
📌 출처 : https://hyeongminlee.github.io/post/bnn001_bayes_rule/
📌 출처 : https://minicokr.com/6
11. Numerical Events and random variable
🔹 Random variable

▢ 우리가 실제 생활에서 관심을 가지고 주로 적용하는 event 는 numerical event 이다.

▢ 숫자로 표현되는 사상에, 해당 값이 나타날 확률을 표본공간에서 구해 표시한 것을 확률 변수 random variable 이라고 한다.
EX. Y = 동전 2개를 던져 나오는 앞면의 숫자 → Y=0,1,2
- Y 의 값은 각각 그 값이 나올 확률을 가지고 있고 확률변수라고 할 수 있다.
- {H,H}, {H,T}, {T,H}, {T,T} → 4가지 사건 중 하나는 sample point 라고 할 수 있다.
- Y=0 : {T,T} → 확률 = 1/4
- Y=1 : {H,T}, {T, H} → 2개의 sample point 가 대응됨 → 확률 = 2/4
- Y=2 : {H, H} → 확률 = 1/4
12. Random Sampling
🔹 표본추출 방법 : design of experiment
▢ 표본을 추출하는 방법은 표본이 가지는 정보에 밀접한 영향을 미친다. 따라서 모수 추정을 위해선 표본추출 방법이 아주 중요하다.
🔹 임의 추출

▢ 각 표본이 뽑히게될 확률이 같은 경우, 표본 추출을 진행하는 것을 random 하다고 이야기 한다.


▢ 모수에 대한 추론을 하기 위해 추출한 표본에 대한 확률을 계산
▢ 확률은 통계적 추론과 통계학의 목적에 맞는 도구이자 근간이다.
'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 스터디 CH7,8,9,10정리 (0) | 2023.03.31 |
|---|---|
| 계량경제학 스터디 CH3,4,5,6 정리 (0) | 2023.03.19 |
| 계량경제학 스터디 CH1,2 정리 (1) | 2023.03.13 |
| Introduction to statistical learning - ch2 (0) | 2022.08.02 |
| Mathematical Statistics with application : chapter 1 (0) | 2022.07.18 |




댓글