🐳 Mathematical Statistics with application 교재를 공부한 내용을 정리하였습니다.
📌 summary
① 통계학의 목표 : 샘플로부터 모집단을 추론
② 추론을 하기 위한 도구 : graphical method, numerical method
③ Probability 는 추론 과정의 메커니즘
What is statistics
1️⃣ Introduction
🔹 통계학의 목적
make an infererence about a population based on information contained in a sample from that population and to provide an associated measure of goodness for the inference
통계학의 목적은 표본 데이터를 추출하고 분석하여 모집단에 관한 추론 방법을 마련하는 데 있다
🔹 기술통계
- 자료를 수집하고 요약정리
- 수치나 표, 그래프 등으로 요약하여 자료의 특징을 파악하는 통계적 방법
🔹 추측통계
- 불확실한 사실에 대한 결론이나 일반적인 규칙성을 이끌어 내는 방법
- 일부를 분석해 관심 대상 전체에 대해 추측하고 일반화 시키는 통계적 방법
*책에서는 추측 통계학의 내용을 이야기하고 있다.
2️⃣ Characterizing a Set of Measurements : Graphical methods
🔹 모집단의 특징을 찾는 과정
▢ 숫자의 집단으로 표현하는 방법을 알아내는 것 = Inference 의 시작
▢ 독립변수들과 종속변수 사이의 관계성 = 종속변수의 모집단 분포에 대해 독립변수들이 미치는 영향
▢ 상대도수 : 총 도수에 대한 각 변량의 도수의 비를 뜻한다. (그 도수의 변량)/(총도수)
🔹 Graphical method


- 그래프로 표현하는 방법은 데이터셋에 포함된 정보의 의미있는 요약치 (summaries) 를 제공한다.
- 통계학의 목적은 모집단에 대한 추론 → distribution plot 을 통해 확률적인 해석을 도출할 수 있다.
- 상대도수 히스토그램에서 선 아래의 영역은 그 사건이 일어날 확률이 된다.
- EX. 모집단으로부터 random 하게 추출된 측정치 measurement 가 2.05 에서 2.45 사이에 위치할 확률은 0.5 → area under the histogram
3️⃣ Characterizing a Set of Measurements : Numerical methods
▢ 상대도수 히스토그램과 같은 그래프는 measurement 의 분포에 관한 유용한 정보를 제공하지만, 히스토그램은 모집단에 관한 추론을 하기에 충분하지 않다.
🔹 Numerical method
▢ sample 에 포함된 정보를 요약할 수 있는 수치적 지표를 생성 → 확률에 대한 언급이 가능 → goodness of inferences
⭐ numerical descriptive measures
① Central tendency
EX. 산술평균
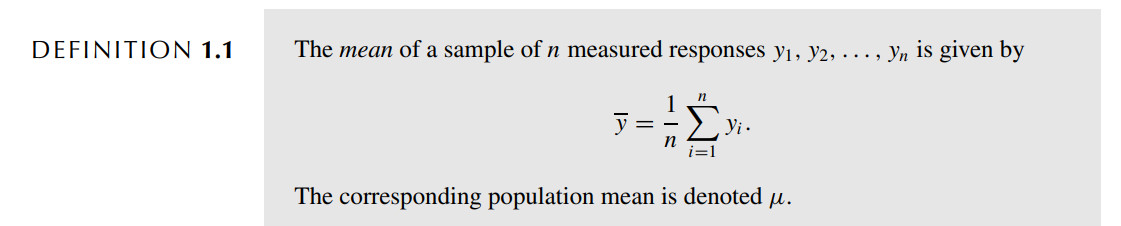
▢ 모평균 μ 는 일반적으로 우리가 알 수 없으며 sample 을 통해 추정 estimate 할 수는 있다.
② Dispersion or variation

▢ n-1 로 나누는 이유는 ch8 에서 자세히 다루지만, 간단하게 설명하자면 n으로 나누는 것보다 모분산에 대한 더 좋은 추정치 (better estimator) 를 제공하기 때문이다.
▢ 분산 값이 클수록 데이터셋 내에서 변동이 크다는 의미이다. 표준편차나 분산의 값이 클수록 평균에서 각 값들이 멀리 떨어져 있다는 의미이므로 그래프의 간격은 넓어지게 된다.

▢ 표준편차 : 분산에 루트를 씌운 값 → 분산은 제곱을 했기 때문에 원래의 계산 단위로 돌려주기 위해 루트를 씌워 계산한다.
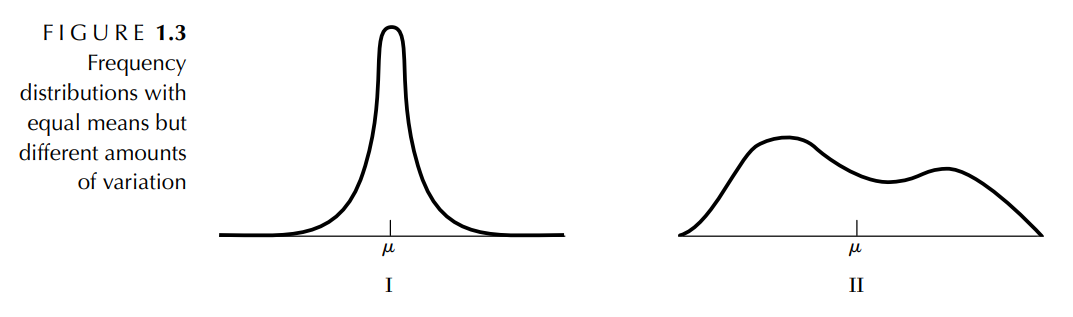
▢ 평균이 같지만 위의 그림처럼 분포 모양이 완전히 다른 경우가 존재한다. 따라서 중심 경향과 퍼짐 경향을 모두 고려해야 데이터의 분포에 대해 이해할 수 있다.
🔹 Empirical rule
통계학에서 68-95-99.7 규칙은 정규 분포를 나타내는 규칙으로, 경험적인 규칙(empirical rule)이라고도 한다. 3시그마 규칙(three-sigma rule)이라고도 하는데 이 때는 평균에서 양쪽으로 3표준편차의 범위에 거의 모든 값들(99.7%)이 들어간다는 것을 나타낸다.

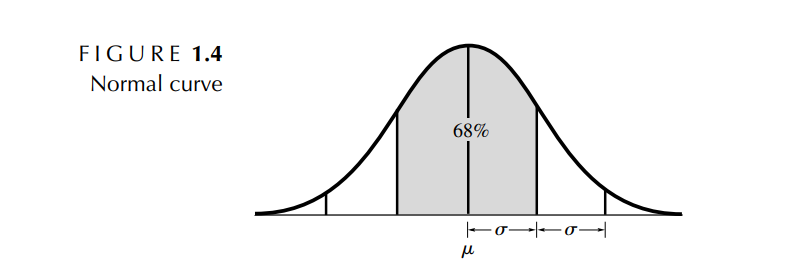
▢ Ex. 수학 점수의 평균이 64이고 표준편차가 10일 때, 점수의 약 68% 는 54점에서 74점 사이에 있음을 알 수 있고, 점수의 약 95%는 44점과 84점 사이에 있음을 알 수 있다 👉 평균과 표준편차는 점수의 도수 분포에 대해 알 수 있는 좋은 지표가 된다.
🐳 연습문제

👉 empirical rule

👉 (mean) - (standard deviation) < 0 이므로 정규분포를 따르지 않는다.

👉 0.84 로 manufacturer 가 주장한 수치보다 4% 더 많은 소들이 증량했다.
4️⃣ How inferences are made
🔹 추론
▢ 모집단의 구조에 대한 이해 + 샘플에 대한 확률 계산을 위한 확률적 이론 사용
▢ 관측된 샘플의 확률을 계산하여 문제를 푸는 것
확률은 통계적 추론의 메커니즘이다.

👉 제한된 정보로 전체를 추정해야 하기 때문에 확실한 것은 알 수 없고 무조건 확률적으로 그 실체를 파악해야 한다는 것. 통계학에서는 최대한 합리적이고 누구나 받아들일 수 있는 기준 하에서 확률을 계산하고 추정한다.
5️⃣ Theory and Reality

'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 스터디 CH7,8,9,10정리 (0) | 2023.03.31 |
|---|---|
| 계량경제학 스터디 CH3,4,5,6 정리 (0) | 2023.03.19 |
| 계량경제학 스터디 CH1,2 정리 (1) | 2023.03.13 |
| Introduction to statistical learning - ch2 (0) | 2022.08.02 |
| Mathematical Statistics with application : chapter 2 (0) | 2022.07.20 |




댓글