Summary
✨ Idea for deep learning for graphs
◾ Multiple layers of embedding transformation
◾ At every layer, use the embedding at previous layer as the input
◾ ⭐⭐ Aggregation of neighbors
✨ Graph convolutional network
◾ Mean aggregaton → permutation invariant/equivariant
✨ Applications of GNNs
◾ Node-Level
◾ Edge-Level
◾ Graph-Level
⭐ GNN is general architecture
◾ CNN and Transformer can be viewed as a special GNN
Pre
✨ 그래프
◾ 점들과 그 점들을 잇는 선으로 이루어진 데이터 구조
◾ 관계나 상호작용을 나타내는 데이터를 분석할 때 주로 쓰인다.
◾ EX. 페이스북 친구관계, 왓챠플레이 유저-영상 감상여부
◾ G = (V,E) 로 정의 , V : 점 집합 , E : 선 집합

◾ 그래프는 주로 인접행렬 adjacency matrix 로 표현된다. (nxn, n은 점의 개수)
◾ 머신러닝에서 그래프를 다룰 땐 점들의 특징을 묘사한 feature matrix (nxf) 로 표현하기도 한다.
✨ 그래프 분석이 어려운 이유
◾ 그래프 크기가 커질수록 사람이 해석할 수 있도록 시각화 하는 것이 어렵다.
◾ 유클리드 공간에 있지 않다 = 좌표계로 표현할 수 없다
◾ 고정된 형태가 아니다 : 아래 두 그래프의 인접행렬은 같다.

✨ 그래프를 사용하는 이유
◾ 관계, 상호작용 같은 추상적인 개념을 다루기 적합
◾ 복잡한 문제를 단순화 시킬 수 있다.
◾ 소셜 네트워크, 바이러스 확산 등의 모델링에 사용 가능
✨ GNN
◾ 그래프에 직접 적용할 수 있는 신경망
◾ 점 레벨, 선 레벨, 그래프 레벨에서의 예측 작업을 수행한다.
◾ 핵심 : 점이 이웃과의 연결에 의해 정의된다.
◾ 모든 점이 각각의 특징을 설명하는 어떤 상태로 표현되어 있다.
ex. 점이 영화이고 판타지,로맨스,공포 중에 판타지와 공포에 해당한다면 (1,0,1) 상태를 가지고 있다.
◾ 연결관계와 이웃들의 상태를 이용해 각 점의 상태를 업데이트 (학습) 하고 마지막 상태 (node embedding) 를 통해 예측 업무를 수행
⭐ cnn, rnn, transformer 와 같은 신경망들은 GNN 의 special 케이스다.
1️⃣ Idea for deep learning for graphs
① Graph
🔘 Graph
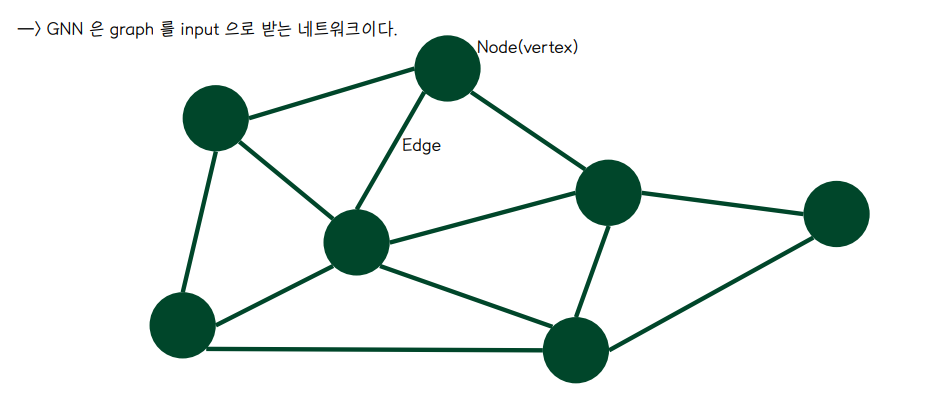
- 관계성을 가지거나 상호작용하는 entity 들을 표현하고 분석할 수 있는 일반적인 언어
- GNN 은 Graph 를 input 으로 받는 네트워크이다.
🔘 Many type of Data are Graphs

- 많은 데이터들은 그래프 형태로 이루어져 있다 👉 네트워크망, 소셜네트워크, computation graph, 분자식
- 그래프 형식을 잘 다룰 수 있는 인공지능이 있다면 유용한 일들을 수행할 수 있을 것이다.
🔘 Modern Deep learning

- cnn,rnn, transformer 들은 간단한 sequence 처리나 grid 처리에 유용하다.
- 그러나 모든 것들이 grid 나 sequence 형태로 존재하지는 않는다 👉 GNN 의 중요성 대두
🔘 Graphs
- 딥러닝 분야의 새로운 개척자로 주목받고 있다.
- 그래프는 무언가를 연결해주는 형태를 가진다.
- ML 에서 가장 핫한 소분야이다.

🔘 Graph Deep Learning is Hard
- graph 를 딥러닝에 적용하는 것은 매우 어렵다. 지금까지 현존하는 딥러닝 네트워크 구조로 구현하기 어렵다.
💨 구현이 어려운 이유 : Network are complex
- 크기가 임의적이다. (Arbitrary size)
- 구조가 복잡하다. (complex topological structure)
- 노드의 순서가 고정되어 있지 않다. (No fixed node ordering)
- reference point 도 고정되어 있지 않다. (No fixed reference point)
- 시시각각 모양이 변하는 구조이다. (dynamic)
- 여러 형태의 feature 들이 하나의 네트워크에 다수 존재한다. (multimodal features) : 가령 아래 그래프에서 빨간점은 item, 회색점은 사람, 노란 점은 오렌지 등등 으로 구성되어 있을 수 있음

② GNN
🔘 Graph Neural Network

- Input : Network (graph)
- Node 들이 Graph convolution layer 들을 거쳐 prediction 을 수행한다.
- 딥러닝처럼 Activation function, Regularization 도 수행한다.
💨 Prediction
- Node label : 새로운 연결노드를 예측
- New link : 노드 사이의 새로운 연결
- Graph : 그래프 자체를 새로 만들거나 subgraph 를 생성
🔘 Node embedding ⭐⭐

- 노드를 d 차원의 임베딩 벡터로 인코딩 👉 비슷한 노드는 임베딩 되었을 때 유사한 벡터로 표현될 수 있도록 노드를 임베딩 한다.
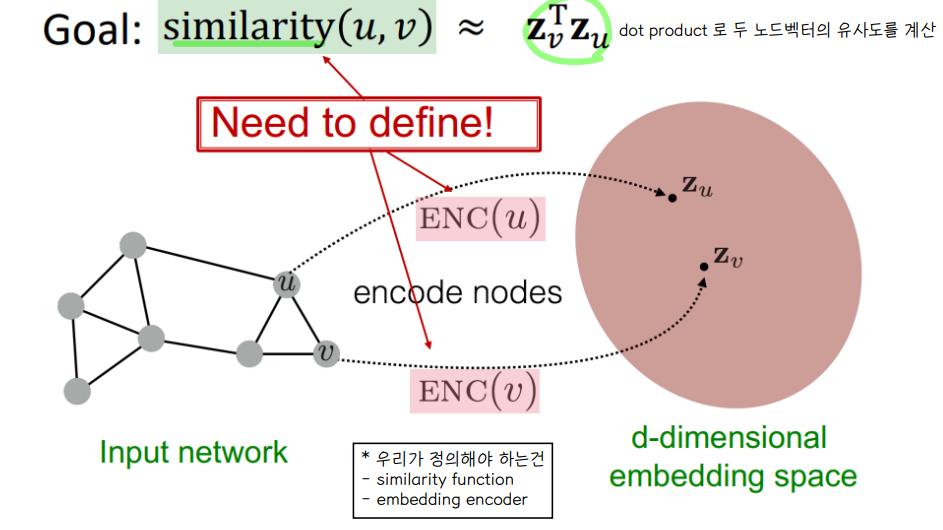
💨 Node embedding 의 목적
- Zu : u 노드를 임베딩한 벡터
- Zv : v 노드를 임베딩한 벡터
- u 노드와 v 노드가 임베딩 되었을 때, 유사도를 dot product 로 측정할 수 있게끔 만든다.
- 비슷한 노드들은 유사도를 높이는 방향으로 임베딩을 수행한다.
- 우리가 정의해야 하는건 유사도함수와 임베딩 인코더
💨 Encoder
- 각 노드들을 저차원의 벡터로 매핑시켜주는 것
- input graph 에서 node v 가 encoder 를 거치면 d 차원의 임베딩 벡터가 된다.
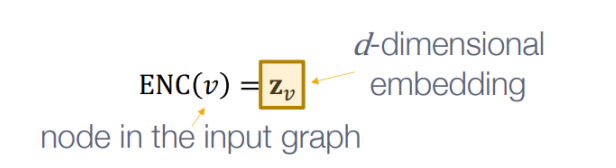

💨 Similarity function
- 벡터 공간에서의 관계성이 original network 의 관계성으로 mapping 되어야 한다.
- original network 의 노드 u,v 의 유사도는 임베딩 된 벡터 공간에서의 두 노드벡터의 dot product 연산 결과와 같다.

🔘 Embedding Table for encoding
💨 가장 단순한 인코딩 방법

- embedding table Z 만들기 👉 table 을 lookup 해오는 방식으로 임베딩 작업을 수행한다.
- row : 임베딩 벡터의 차원 (dimension of embeddings)
- column : node 의 총 개수
- 어떤 노드에 대한 임베딩 벡터를 얻고싶으면 그 노드에 해당한느 칼럼을 읽어오기만 하면 된다.
💨 한계점
- 그러나 위와 같은 방식으로 인코딩을 하게 되면, 노드가 증가할수록 table 크기가 linear 하게 증가한다는 단점이 존재한다.
- 또한 노드 간에 파라미터를 공유하는 것이 없어 , 노드 개수가 증가하면 연산량이 증가하게 된다. CNN 의 경우엔 receptive field 마다 filter 의 weight 파라미터를 공유했음!
- 훈련 과정 중에 보지 못했던 노드들에 대한 임베딩을 진행할 수 없다 👉 5명의 가입자에 대한 노드 임베딩 벡터가 존재했는데, 한 명이 신규가입을 하면 그 유저에 대해서는 노드 벡터가 존재하지 않음. 즉, 훈련 당시에 생성된 임베딩 테이블에는 신규 노드에 대한 정보 자체가 존재하지 않으므로 임베딩이 불가능하다 👉 그러나 network 의 가장 큰 특징 중 하나가 dynamic 하다는 점인데 이와 상충함
🔘 Deep Graph Encoders
- 임베딩 테이블을 구축하는 방법 대신, 딥러닝을 사용하여 인코딩을 수행한다.
- 여러개의 노드들이 Neural network 를 거쳐 node embedding 을 형성한다 👉 임베딩 결과를 가지고 여러가지의 task 들을 수행한다.

🔘 Tasks on Networks
- Node classification : 노드의 타입을 분류(예측)
- Link prediction : 유사도가 높은 노드들은 엣지로 연결되어 있을 가능성이 높다는 가정하에 두 노드 사이의 링크 연결성을 예측
- Community detection : 긴밀하게 연결된 노드 집단 node cluster 가 있는지 여부를 밝힘
- Network similarity : 두 네트워크의 유사도를 측정
③ deep learning for graphs
🔘 Setup
- G : graph
- V : 점들의 집합
- A : adjacency matrix 👉 두 노드가 연결되어 있느냐를 binary 형태로 알려주는 matrix

- X : matrix of node features (m x |V|) 👉 m 은 node 하나에 들어있는 feature 개수를 의미한다.
- ex. user node → gender, age, height
- v : node in V
- N(v) : 이웃노드 집합 ex. N(A) = {C,D,B}
- Node feature
- social networks : user profile, user image
- Biological networks : gene functional information
🔘 A Naive Approach
- adjacency matrix 와 feature 를 concatenation
- concat 한 행렬을 fully - connected network 에 입력한다.
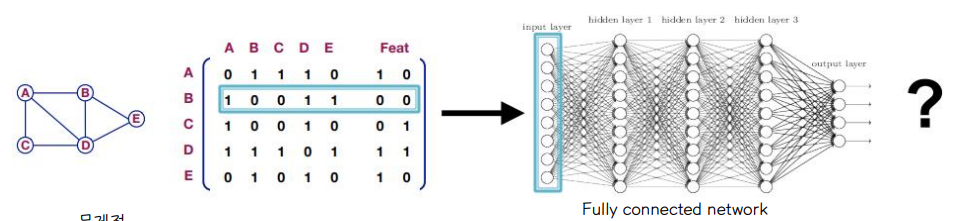
👉 그러나 이러한 접근방식에는 문제점이 존재한다.
- ܱ O(|V|) parameters : 파라미터 개수가 노드의 개수가 증가할수록 linear 하게 증가한다.
- 그래프 사이즈가 다른 경우에 적용이 불가능하다 : 만약 5개의 노드로 훈련된 네트워크에 6개 노드로 이루어진 input 이 들어오면 훈련이 불가능
- 딥러닝은 node 의 순서에 민감하다 : node 가 그림처럼 A,B,C,D,E 순서로 훈련되면 그 이후에 들어오는 input 도 같은 순서로 들어와야 한다. 딥러닝 네트워크에서는 같은 그래프더라도 들어오는 노드 순서가 다르게 들어오면 다른 훈련 결과를 내놓는다.
그래서 이런 단순한 접근 보다는 앞으로 살펴볼 GNN, GCN, GAT 등의 모델이 등장했다.
2️⃣ Graph convolutional network
핵심 Idea : node 의 이웃이 계산된 그래프를 결정한다.
📌 https://jxnjxn.tistory.com/77
[CS224W] 8. Graph Neural Networks
업로드가 조금 늦어졌습니다. ㅎㅎ 8강은 성실함의 대명사 이재빈님께서 리뷰하셨습니다. Graph에 Neral Network, GNN을 적용하는 강의 입니다. 크게 Graph에 Deep learning을 적용하는 개요와, Neighborhood aggr
jxnjxn.tistory.com
① generalize CNN
🔘 CNN

- spatial feature를 계속해서 layer마다 계속해서 추출해 나가면서 고차원적인 특징을 표현
- grid 구조 외에 다른 구조에서 CNN 을 적용시켜보자
💨 합성곱 연산의 아이디어
- local connectivity, shared weights, use of Multi-layer
- 주변 정보를 변환하고 이를 결합한다 👉 Graph neural network 에 적용

🔘 Real-World Graphs
- 그러나 CNN 을 graph 에 적용시키고자 할 때, 실제 다루는 그래프 모습은 아래와 같기 떄문에 몇가지 고려해야할 사항이 존재한다. (그래프의 구조적 특성 때문에 기존의 합성곱 연산을 적용하는데 어려움 존재)

- graph가 dynamic + complex structure 한 특성을 가지고 있기 때문에 다양한 size 를 가진 sliding window 를 사용해야 한다.
- permutation invariant : 그래프는 순서에 영향을 받지 않는다. (모델 출력에 입력 벡터의 순서가 영향을 미치지 않는 데이터)
🔘 Permutation Invariance

- Graph 는 does not have a canonical order of node 즉, 노드 사이에 정해진 순서가 없는 구조를 가지고 있는데, Neural Network 에 입력되는 행렬 (feature matrix, adjacency matrix) 은 노드의 순서 설정에 따라 형태가 달라진다.
- ⭐ 따라서 "Graph 의 노드 간 순서는 존재하지 않는다" 라는 특징을 반영해주기 위해 순서에 강력한 permutation invariant 함수 f 를 도입한다.

- f(A1, X1) = f(A2, X2) 👉 즉, 노드에 A~F 까지 이름 순서를 부여할 때 왼쪽 plan 과 오른쪽 plan 처럼 다양하게 존재할 수 있지만 그에 상관 없이 permutation invarianct 한 함수 f 는 동일한 결과를 도출해낸다.
- 혹은 f(graph with permutation) = graph without permutation 이 성립하면 된다. f(p.G) = f(G)
🔘 Permutation Equivariance
- graph 에 permutation 을 한 후 f 를 적용한 것과 graph 를 f 에 넣고 이후에 permutation 한 것이 같으면 permutation equivalent 라고 한다.
- f(graph with permutation) = permutation * f(graph)


⭐ GNN 은 permutation invariant 와 equivalent 둘 다 모두 만족하는 function 으로 이루어져 있어야 한다
② GCN
🔘 GNN Overview
- GNN 은 다수의 permutation equivariant/invariant 함수로 구성되어 있다.

- 다른 neural network 구조는 permutation invariant/equivariant 하지 않는다.
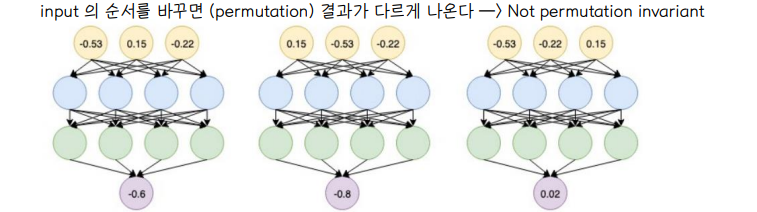

🔘 Graph Convolutional Networks
⭐ Computation graph, information propagate and transform
- Idea : Node's neighborhood defines a computation graph 👉 네트워크 이웃들이 computation graph를 정의
- Learn : how to propagate information across the graph to compute node features 👉 node feature 를 계산하기 위해 그래프 전반에 걸쳐 정보를 전파하는 방법을 배운다.

- 이웃 노드들의 정보를 합산 : reference node 와 주변 node 의 weighted sum
- 모든 노드들은 노드마다 인접 노드들에 기반하여 computation graph 를 정의한다.
- 노드의 새로운 feature 를 계산하기 위해 computation graph 에서 형성된 노드들로부터 데이터를 aggregation 한다.
🔘 Aggregation Neighbors
- Generate node embeddings based on local network neighborhoods 👉 local 범위의 이웃 노드들로부터 node 임베딩을 생성한다.
- Nodes aggregate information their neighbors using neural networks 👉 NN을 사용하여 주변 이웃 노드들로부터 정보를 집계한다.
- 모든 노드들이 자기만의 Neural Network Architecture를 갖고 있으며, 각자의 neighborhood에 근거해 computiation graph를 정의

👉 왼쪽의 input graph 를 오른쪽 처럼 펼처서 A 를 예측하는 2-layer NN 으로 만듦
👉 노드 A에 대한 feature를 A의 이웃 노드 정보를 NN으로 수집해서 나타냄
- Network neighborhood defines a computation graph 👉 network 의 주변부가 computation graph 를 만든다
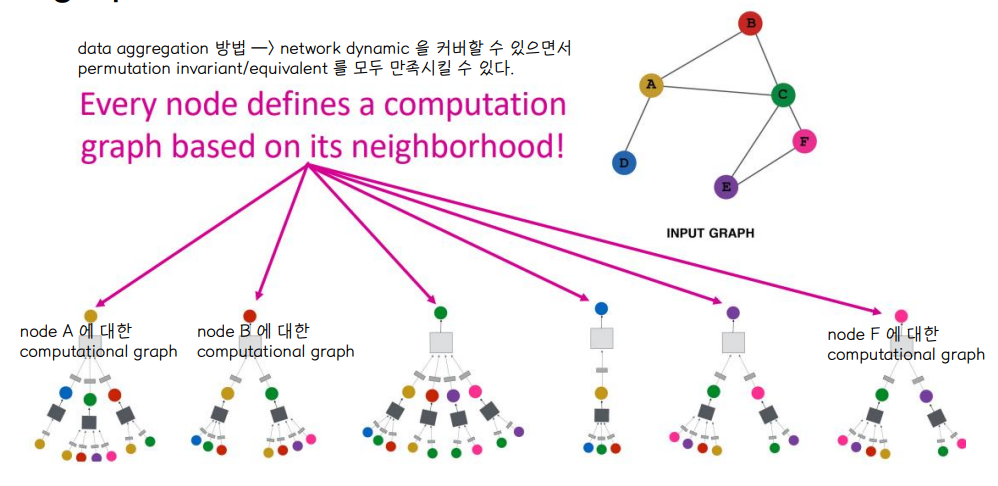
⭐ 모든 노드에 대해 각각 computation graph가 생성된 모습 , 네모 회색 박스들이 Neural Network 를 의미함
⭐ permutation invariant/equivalent 함수로 순서에 상관없는 집계함수인 '평균' 을 주로 사용한다.
🔘 Deep model : many layers
- model 은 임의의 depth 를 가질 수 있다 👉 graph 에는 hop 이라는 단위가 있다
- hop 크기와 layer 개수가 비례
- 노드들은 각 layer 마다 임베딩을 가진다.
- Layer-0 embedding of node v is its input feature Xv
- Layer-k embedding gets information from nodes that are ݇k hops away : node 로부터 k hop 떨어진 곳으로부터 정보를 받아 임베딩을 수행하는 층
⭐ Layer-K 를 사용해서 임베딩을 수행 = K-hop 만큼의 노드정보를 가져왔다는 의미
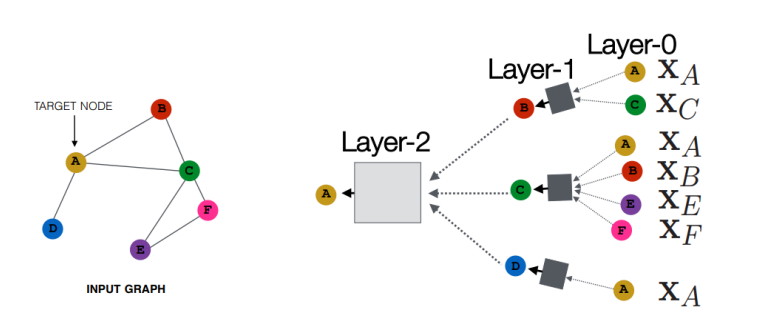
🔘 Neighborhood aggregation
- 이웃에서 정보를 집계해 가져오는 단계에서 어떻게 합산해오느냐에 따라 네트워크 종류가 구분된다.
- 이때 집계하는 함수는 그래프의 특성인 permutation invariant 를 고려해야 한다.
- 기본적으로 이웃에서 집계한 정보를 average (평균) 해서 NN에 적용하는 방법을 많이 사용한다.
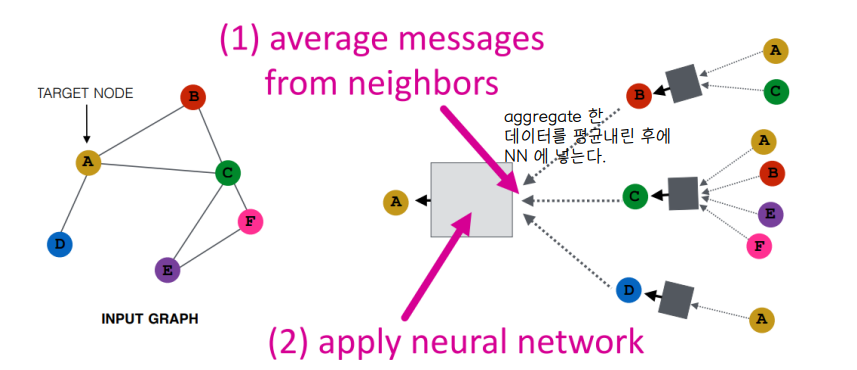
🔘 Neighborhood aggregation : The math
- Encoder를 수식적으로 나타내면 다음과 같이 정리



- hv(0) = Xv : 0-th layer embedding 값은 node feature 값과 동일하게 초기화한다.
- hv(k) = k-th layer (k-hop) embedding 👉 Wk 와 Bk 는 학습시키는 파라미터 weight matrix
- Zv : 네트워크의 최종 계층에서의 embedding 표현으로 이웃에 대한 정보 집계를 k-layer 를 통과한 후의 값
⭐ 네트워크가 깊을수록 성능이 좋다 → 더 큰 네트워크에서 더 많은 정보를 집계함
- Wk,Bk : 같은 weight 를 공유한다.
- Wk : 이웃노드들로부터 집계한 정보에 대한 가중치
- Bk : 지금 보고 있는 노드의 이전 레이어에서의 임베딩 정보에 대한 가중치 (자기 자신의 변환을 위한 가중치 행렬)
- 이웃정보에 집중할지, 자신의 own property 에 집중할지 결정한다.
⭐ 최종 layer 에서의 node embedding 을 loss function 에 넣고 SGD 를 이용해 학습을 진행한다.
🔘 Equivariant Property
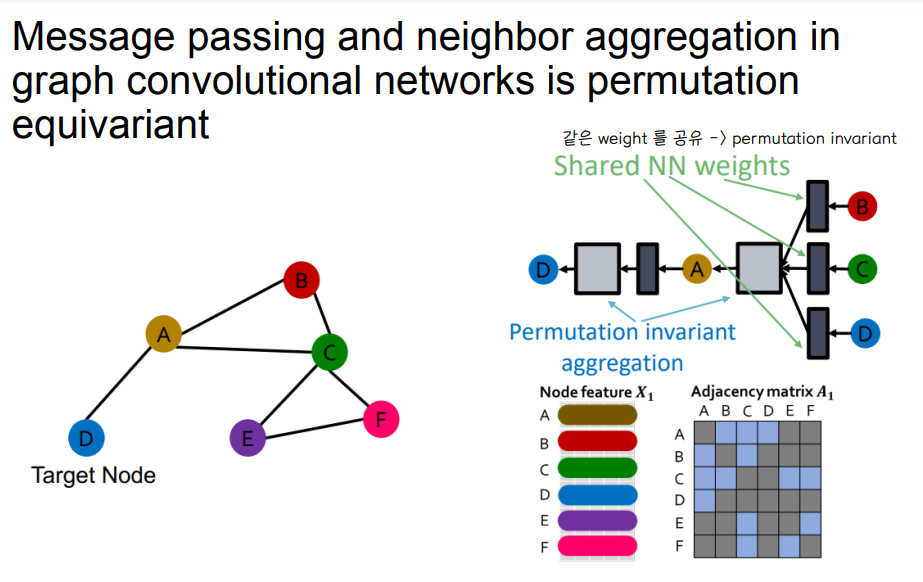
- neighbor aggregation in graph convolutional networks is permutation equivariant
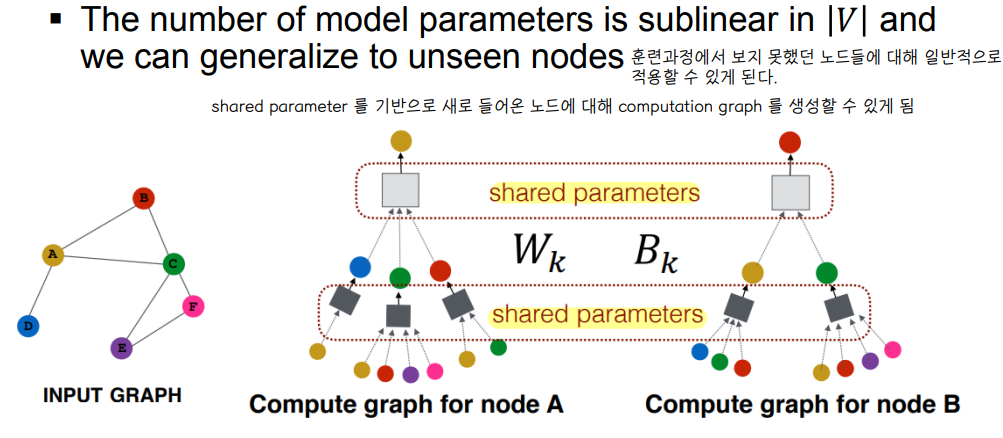
🔘 Inductive Capability
⭐ Aggregation parameters들이 모든 노드들에 대해 공유된다. 같은 층의 신경망은 학습 가중치를 공유한다.
- 새로운 노드를 만들 수 있는 능력 : CNN의 특징이기도 한, 이렇게 파라미터를 공유하는 특징을 가지고 있기 때문에 unseen node 정보에 대해서도 어느정도 알 수 있다.
- same aggregation parameters are shared for all nodes
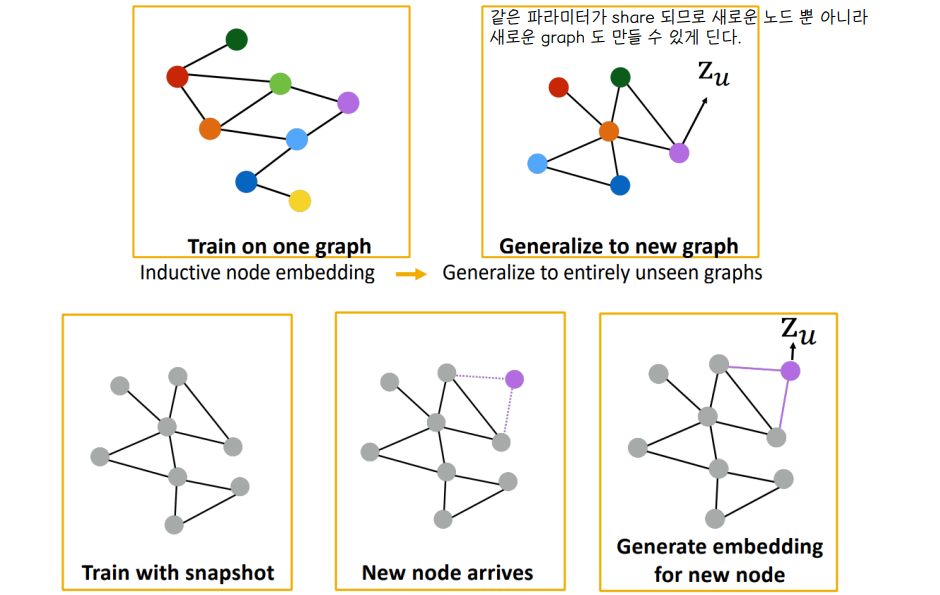
- 한가지 그래프에 대해서 학습을 하고, node embedding하는 법을 배워서 새로운 그래프에 대해서 일반화 할 수 있다.
3️⃣ Applications of GNNs
① Node-Level Application
🔘 Protein Floding



- 노드 : 아미노산 순서
- 엣지 : 아미노산 사이의 거리
- 유기체 A의 단백질 상호작용 그래프에서 학습한 모델을 통해 새롭게 취득된 데이터인 유기체 B의 임베딩을 생성
② Edge-Level Application
🔘 RecSys
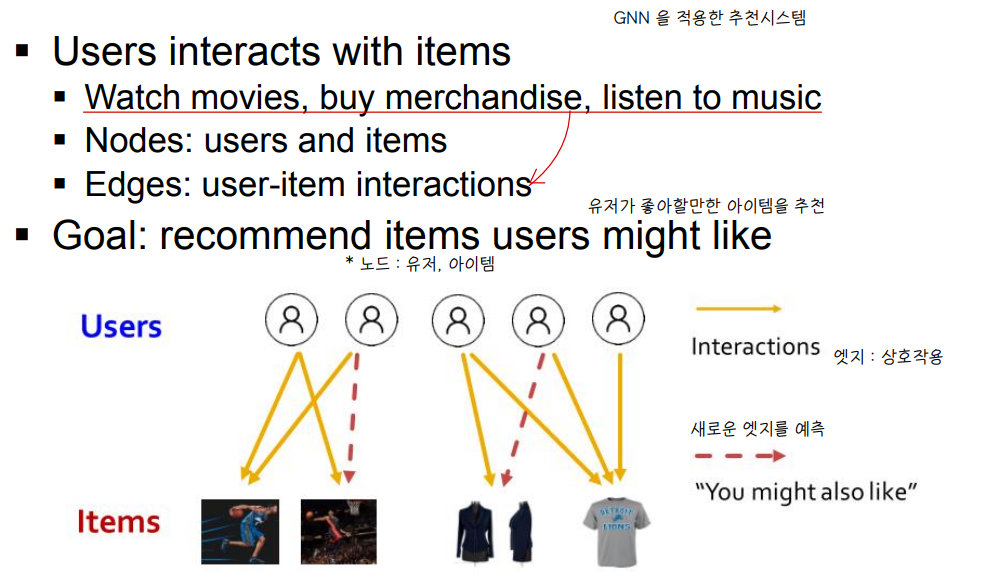

- 새로운 edge 를 예측 👉 유저가 좋아할만한 아이템을 추천
③ Graph-Level Application
🔘 Drug Discovery

- 새로운 분자구조 생성
'1️⃣ AI•DS > 📒 딥러닝' 카테고리의 다른 글
| [인공지능] Meta learning , Transfer learning (0) | 2022.06.14 |
|---|---|
| [인공지능] Reinforcement Learning (0) | 2022.06.14 |
| [인공지능] 추천시스템 (0) | 2022.06.13 |
| [인공지능] GAN (0) | 2022.06.13 |
| [인공지능] Transformer Models (0) | 2022.06.11 |




댓글