📌 교내 '인공지능' 수업을 통해 공부한 내용을 정리한 것입니다.
요약
① multiple layer 가 필요한 이유
- XOR 문제
- feature extraction and classification
② Multi-layer perceptron
- gradient descent
- backpropagation algorithm
1️⃣ MLP
① MLP란
👀 Perceptron vs Multi layer Perceptron
- Perceptron : 뉴런이 하나만 존재하는 경우

- MLP (multi-layer perceptron) : 뉴런(퍼셉트론)이 여러개가 존재하며 층을 이룬다.
- layer : 뉴런과 뉴런 사이의 시냅스 층을 지칭함

🤔 뉴런이 열거된 부분을 layer 라고 칭하며 hidden layer 라고 설명하는 경우도 있으나, 수업에선 시냅스 연결부분을 layer 로 지칭함
② MLP
👀 input layer


⭐ weight matrix W 차원 : (output) x (input)
👀 Output layer


👀 MLP

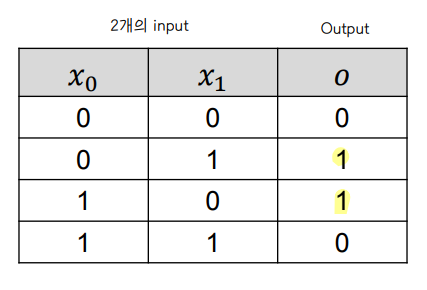
③ XOR 문제
👀 XOR 문제
- 들어오는 input 이 다를 경우에만 output 을 1로 도출하는 문제
👀 단일 퍼셉트론을 가지고 XOR 문제를 풀 수 없다.
- AND 문제는 단일퍼셉트론을 가지고 풀 수 있다.
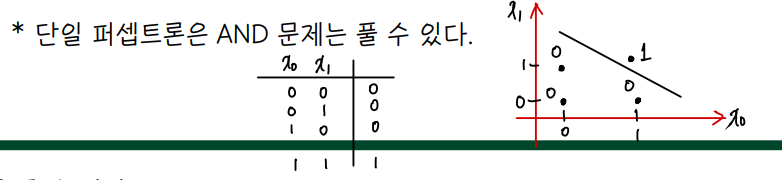
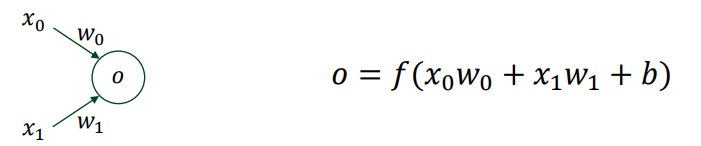

- 뉴런이 하는 역할은 input 에 대해 구분을 짓는 초평면 (hyperplane) 을 그리는 것으로, 선은 가중치 w와 편차 b에 의해 결정된다. 선을 기준으로 0 또는 1의 output 을 생성해낸다. (classification)
- input 이 위와같이 (x1, x2) 2개가 아닌 (x1, x2, x3) 이렇게 3개면 3차원 공간에서 2차원 평면을 그린다.
⭐ 하나의 뉴런은 n 차원 공간에서 n-1 차원의 초평면을 그려주는 역할을 한다.
👀 다층 퍼셉트론 MLP 로는 XOR 문제를 풀 수 있다!
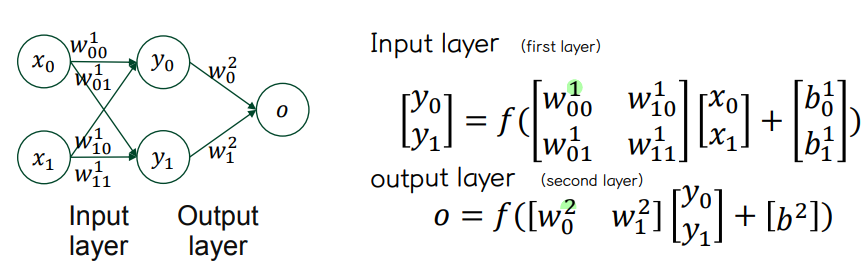
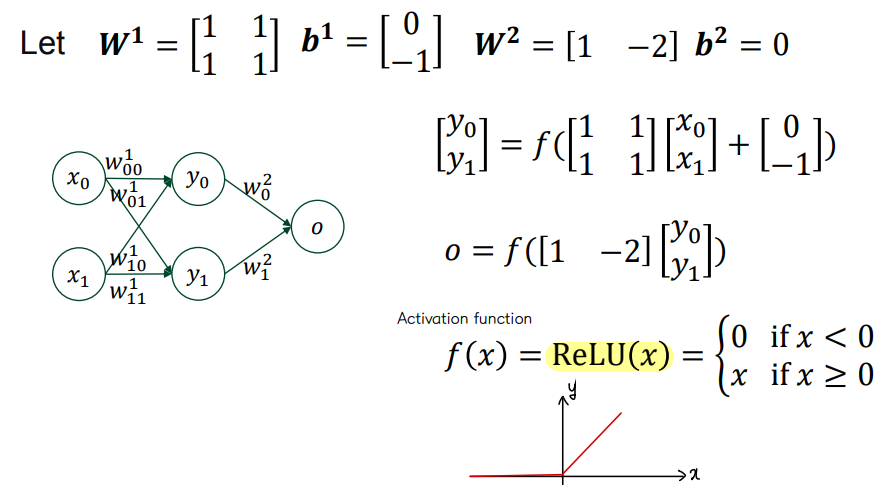
- 아래와 같이 가중치와 편차의 초기값을 설정하고, 활성화 함수를 ReLU 로 계산해보자
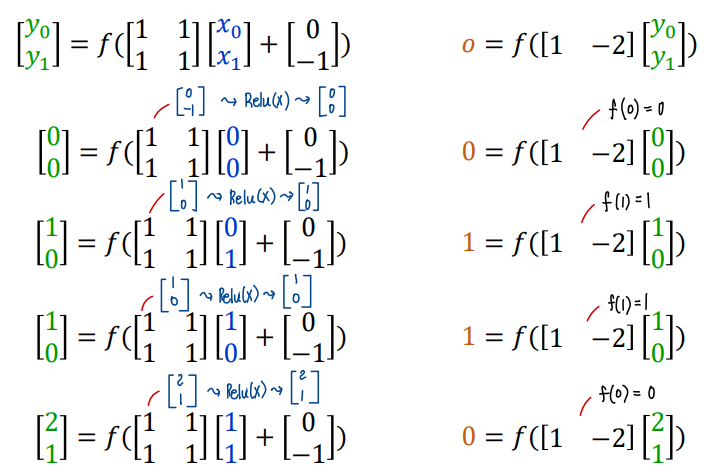
- batch 형태로 input 을 표현해보기

④ 중요!
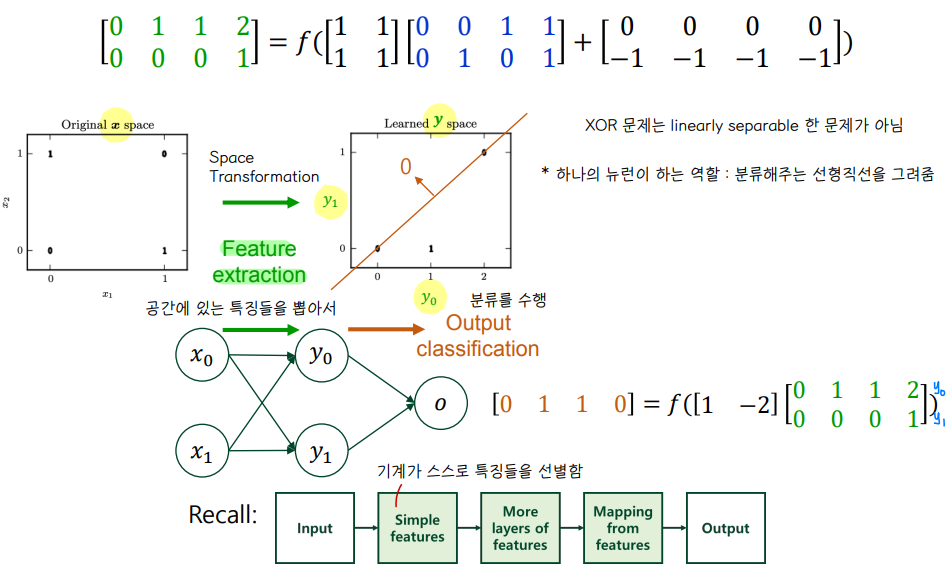
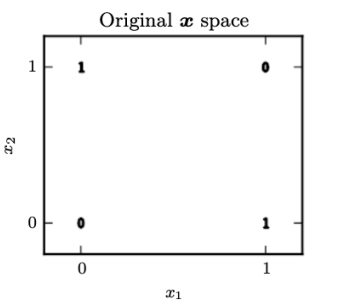
- XOR 은 linearly separable 한 문제가 아니다.
- 따라서 본래 (x1,x2) 공간으로부터 가중치와의 연산을 통해 공간에 있는 특징 (y1,y2) 을 추출하고 추출한 공간으로부터 분류 문제를 수행하면 XOR 문제를 풀 수 있게 된다.
- Feature extraction & output classification
- 하나의 뉴런이 하는 역할 : 분류해주는 선형 직선을 그려준다.
2️⃣ MLP training
* 위에서 정의한 W,b 초기값은 XOR 문제를 한번에 잘 풀기위해서 임의로 설정한 값이었다.
* 그럼 어떻게 하면 분류를 잘 수행해내는 W,b 행렬을 만들 수 있을까?
① Gradient descent
👀 MLP 훈련 = 주어진 데이터를 통해 목표를 달성해낼 수 있는 W,b 행렬을 찾는 것
- Cost function 👉 analytically 하게 (미분) 연산하는 것은 불가능하므로 gradient descent 방법을 사용한다.
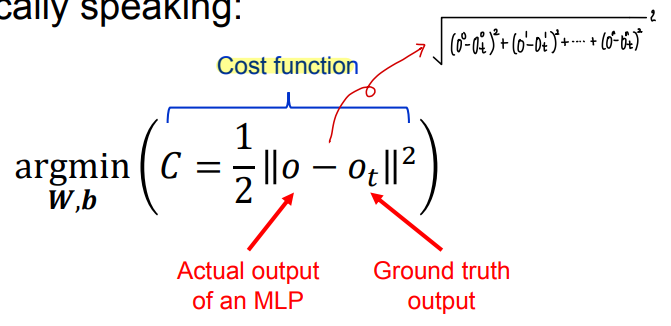

- 가중치에 대하여 cost function 을 편미분한다.
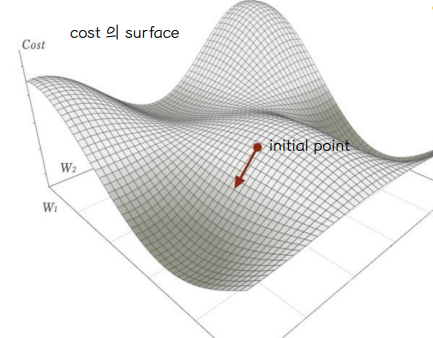
👀 단일 퍼셉트론에서의 gradient descent 연산

👀 다층 퍼셉트론에서의 gradient descent 연산
- i : input unit 의 개수 , j : hidden unit 의 개수, k : output unit 의 개수
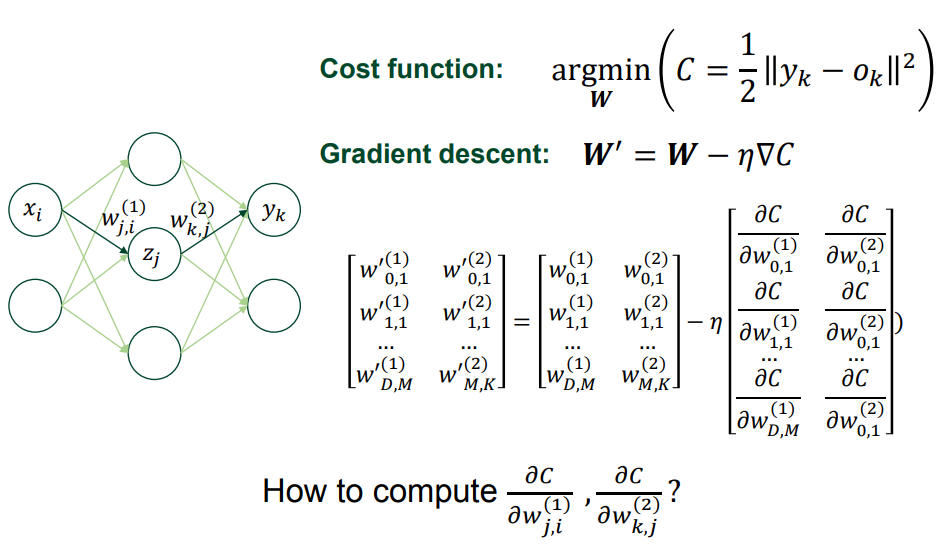
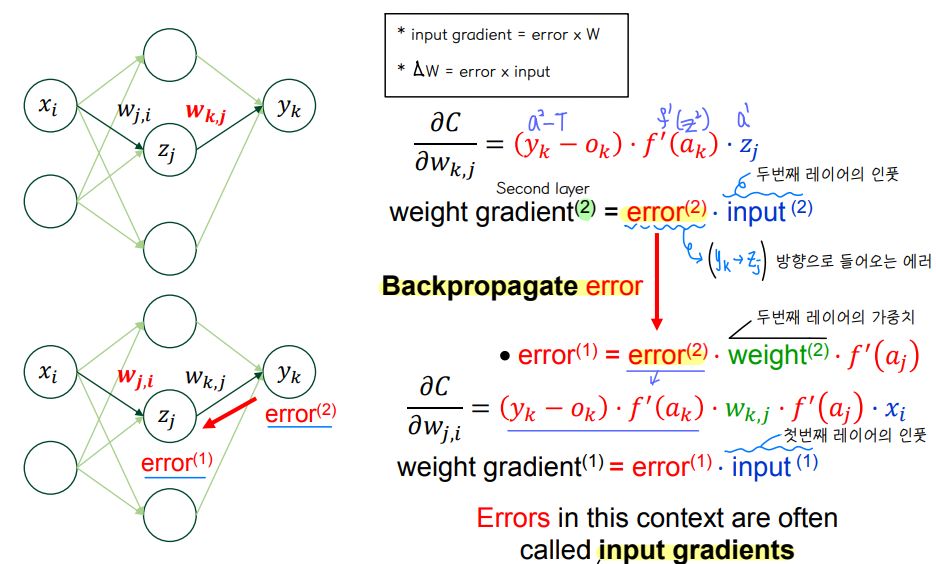
- input gradient : 직전에 발생한 error 와 weight 를 곱한값
- weight gradient : error x input
👻 참고
- bias 에 대한 미분값도 기억하기!
- 활성화함수 미분 곱에서 행렬곱 연산과 element wise 곱셈 연산을 주의할것!
# error(2)
dA2 = np.multiply(dMSE(A2, T), self.second_layer_dactivation_func(Z2))
# weight gradient = error(2) * input
dW2 = np.dot(A1.T, dA2)
# bias gradient
dB2 = np.sum(dA2, axis=0, keepdims = True) ## error(2) 를 열방향으로 덧셈
# error(1)
dA1 = np.multiply(np.dot(dA2, self.second_layer_weights.T), self.first_layer_dactivation_func(Z1))
# weight gradient = error(1) * input
dW1 = np.dot(X.T, dA1)
# bias gradient
dB1 = np.sum(dA1, axis=0, keepdims = True) ## error(2) 를 열 방향으로 덧셈
👀 MLP output 이 2개 이상인 경우
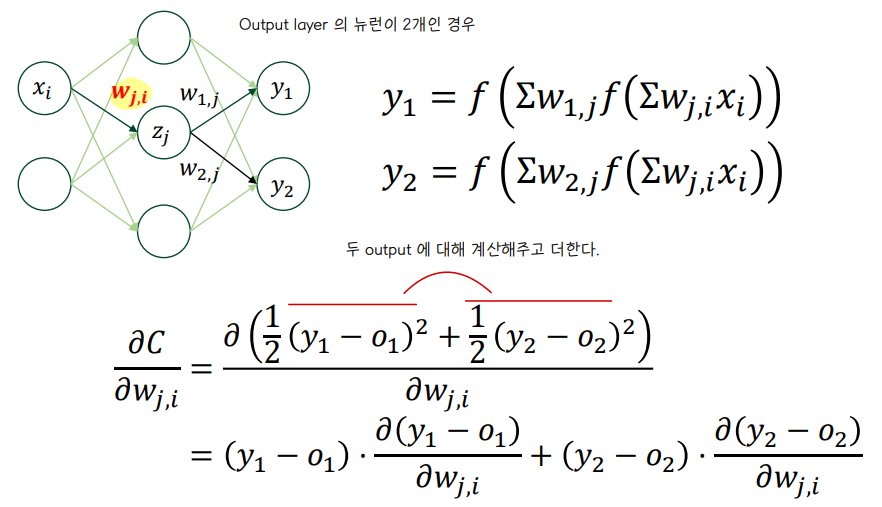
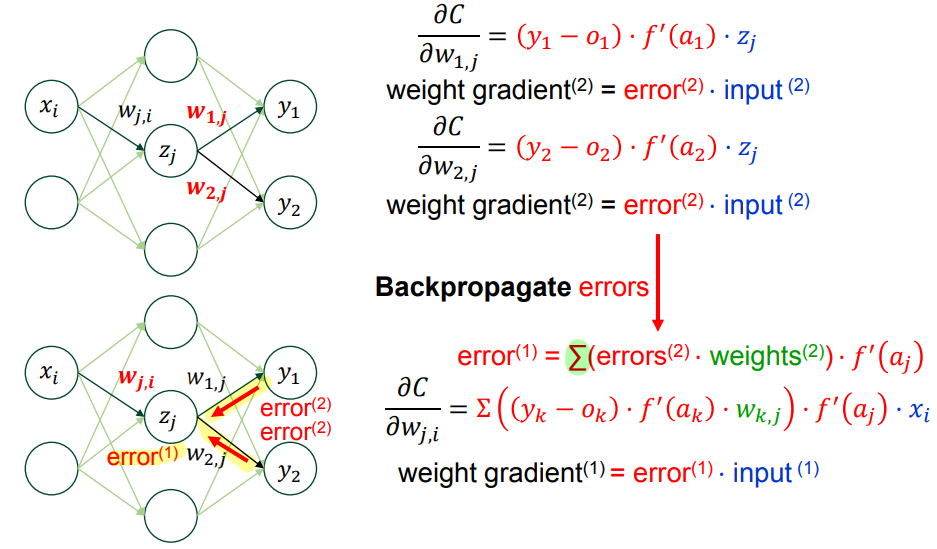
② Backpropagation
👀 연산 과정

1. W, b 를 작은 값으로 초기화
2. training set 전체에 대해 아래의 연산을 수행 (1 epoch 기준)
a. Forward Propagation : output 값과 error 를 계산
b. Backpropagation : error 를 역전파 한다.
c. W,b 를 업데이트한다.
3. 신경망이 잘 훈련될때까지 2번을 반복한다.
* example 꼭 손으로 직접 계산해보기
'1️⃣ AI•DS > 📒 딥러닝' 카테고리의 다른 글
| [인공지능] Training CNN (0) | 2022.04.26 |
|---|---|
| [인공지능] CNN (0) | 2022.04.23 |
| [인공지능] DNN (0) | 2022.04.23 |
| [인공지능] Basic Neural Network (0) | 2022.04.21 |
| [인공지능] Introduction to AI/Deep learning (0) | 2022.04.21 |




댓글