👀 계량경제학 개인 공부용 포스트 글 입니다.
3장. 이치에 맞는 회귀분석 구성
① 회귀분석의 근본 원칙
a. 서론
• 처치집단과 통제집단 간의 차이를 추정하는 계산 방법으로서 회귀모형
• 회귀분석에서는 설명변수들이 통제될 수도 혹은 통제되지 않을 수도 있다.
• 무작위 배정의 도움이 없는 경우, 회귀분석의 추정치들은 인과관계로 해석될 수도 있고 그렇지 않을 수도 있다.
• 어떤 조건 하에서 회귀분석의 결과가 인과관계로서 해석될까
• 회귀 추정치들의 특성들에는 모집단 회귀함수 (population regression function) 와 조건부 기대함수 (conditional expectation function) 사이의 밀접한 관계와 회귀추정치의 표본분포가 포함되어 있다.
b. 경제적 관계과 조건부 기대함수
• 조건부 기대함수 conditional expectation function CEF : E(Yi | Xi) → Xi 의 함수
• CEF 를 보완하는 하나의 중요한 개념은 the law of iterated expectations 반복기댓값 법칙이다.
↪ E[Yi] = E{E[Yi | Xi]}
↪ 반복 기댓값 법칙에 의해 우리는 하나의 확률변수를 CEF 와 잔차라는 두 부분으로 분해할 수 있다.
↪ Yi = E[Yi | Xi] + ϵi : Xi 에 의해 설명되는 CEF 부분과 Xi 의 모든 함수와 직교하는 (상관관계가 0인) 잔차 부분으로 분해될 수 있다.
• CEF 의 예측 특성 : CEF 는 Xi 가 주어졌을 때, Yi 의 MMSE (minimum MSE) 예측치이다.
• CEF 의 특성 : ANOVA 분산분석 정리 : V(Yi) = V( E(Yi | Xi) ) + E( V(Yi | Xi) )
C. 선형회귀모형과 CEF
• 회귀분석은 CEF 와 밀접하게 연결되어 있고 실증적 관계를 자연스럽게 요약해준다.
• 모집단 잔차는 설명변수인 Xi 와 상관관계가 0이다. 오차항은 스스로 아무런 역할을 하지 못한다. β 가 주어져야만 오차항이 존재할 수 있고, 의미를 가질 수 있다.
• βk = Cov(Yi, x_ki) / V(x_ki)
• CEF 가 선형이라고 가정하면, 모집단 회귀함수가 CEF 이다.
• Xi 의 '모든' 함수들 중에서 CEF E[Yi | Xi] 가 Yi 에 대한 최적 에측치인것처럼 모집단 회귀함수는 선형함수들 중에서 우리가 구할 수 있는 최적 함수이다.
• CEF 가 종속변수의 최적 무제약 예측치인 것처럼, 회귀 모형은 종속변수에 대한 최적 선형 예측치를 제공한다.
• 회귀모형의 CEF 정리를 재해석하면, 회귀계수들은 개인의 Yi 가 아니라, E[Yi | Xi] 를 종속변수로 사용하는 경우에도 구할 수 있다.
d. 점근적 OLS 추론
• 최소제곱 ordinary least squares : OLS 추정량
• 대수의 법칙 : 표본 적률은 그에 대응하는 모집단 적률에 확률적으로 수렴한다. 충분히 큰 표본을 구성하는 방법을 통해, 표본 평균이 모집단 평균에 가까울 확률을 원하는 만큼 높게 만들 수 있다.
• 중심극한정리 : 표본적률은 점근적으로 정규분포를 따른다.
• 슬러츠키 정리

• 연속사상 정리 : 확률극한은 연속함수에 그대로 적용된다.
• 델타법 : 정규분포에 근사하는 벡터형 확률변수를 생각해볼 때, 연속적이면서 미분가능한 스칼라 함수 역시 점근적으로 정규분포를 따른다.
• 점근표준오차를 "robust" 한 표준오차라고 부른다. 이 표준오차를 강건하다고 말하는 이유는 충분히 큰 표본에서 이 표준오차를 사용하면 자료와 모형에 관한 최소한의 가정만으로도 정확한 가설 검정과 신뢰구간 설정이 가능하기 때문이다.
• 선형 확률모형 linear probability model LPM : 선형 확률모형은 노동시장 참가 여부와 같이 종속변수가 더미변수로서 0 또는 1의 값만을 갖는 회귀모형을 말한다. 필연적으로 LPM 의 잔차는 이분산성을 갖는다.
• 고전적인 정규 회귀모형이라고 불리는 전통적인 방식에는 고정된 (비확률적) 설명번수, 선형 CEF, 오차의 정규분포, 그리고 등분산성을 가정한다.
e. 포화된 모형, 주효과 및 기타 논의
• saturated 포화된 , main effects 주효과
• 포화된 회귀모형은 설명변수가 이산변수인 회귀모형이다. 이 모형에서는 설명변수가 취할 수 있는 모든 가능한 값들에 대해 각각 모수를 부여한다.
• ex. 설명변수로서 근로자의 대학 졸업 여부를 표시하는 변수 하나만이 있는 모형에서 대학 졸업 여부라는 한 개의 더미변수와 상수만을 포함하고 있는 모형은 포화된 모형이다. 설명변수가 여러개의 값들을 취하더라도 포화된 모형을 만들 수 있다.
• 포화된 회귀모형은 CEF 를 완벽하게 추정한다. CEF 는 모형을 포화시키는 데 사용한 더미변수들의 선형함수이기 때문이다.
• 만약 두 개의 설명변수가 (대학졸업여부를 나타내는 더미변수, 성별을 나타내는 더미변수) 있다면, 이 모형은 두 개의 더미변수, 더미변수들 간의 곱 그리고 상수를 포함하는 경우에 포화된다. 더미변수들에 대한 계수들을 main effect 주효과 라고 하고 더미변수들의 곱을 interaction term 교차항 이라고 한다.
• 포화된 모형을 가지고 먼저 분석을 시작하는 것이 자연스럽다. 포화모형은 CEF 의 근사치를 제공하기 때문이다.
② 회귀모형과 인과관계
• 어떤 경우에 회귀계수를 실험으로부터 도출되는 인과효과의 근사치라 생각할 수 있을까?
a. 조건부 독립성 가정
• 회귀분석의 결과가 인과적으로 해석되는 경우 ⇨ 근사하는 CEF 가 인과적으로 해석될 때
• 조건부 독립성 가정 CIA (conditional independence assumption) : 회귀 추정치가 인과적으로 해석될 수 있도록 정당성을 제공하는 핵심 가정이다.
↪ 2개 이상의 확률변수가 특정 조건에서 서로 독립적이라는 것을 전제로 한다 : P(A,B | C) = P(A|C)*P(B|C)
↪ 고정될 필요가 있는 통제변수들을 우리가 사전에 알고 있거나 관측할 수 있다고 가정한다.
출처 (설명이 매우 잘 되어있다)





• CIA 는 관측된 특성들 Xi 가 주여졌을 때, 즉 Xi 가 동일한 사람들 사이에서 선택편의가 사라진다고 가정한다 : {Y0i, Y1i} ⫫ ci | Xi
↪ ci : 처치변수
• 많은 무작위 실험에서는 CIA 가 충족된다. Xi 가 주어진 조건 하에서 si 가 무작위로 배정되기 때문이다.
• EX. CIA 가 성립할 경우에는 동일한 Xi 를 갖니 사람들에 대해 학력수준별로 평균임금을 비교하는 것이 인과적 해석을 가능하게 한다.
• 무조건부 평균효과는 모든 개체를 대상으로 평균적인 인과처리 효과를 나타내는 지표이다. 평균인과효과는 처리받은 그룹 내에서의 평균적인 인과효과를 나타내므로 서로 구별되는 상이한 개념이다. 무조건부 평균효과는 X에 고유한 인과효과들을 Xi 의 주변분포 (marginal distribution) 을 이용해 가중한 평균을 구함으로써 계산한다.
• matching estimator : 동일한 Xi 값을 가진 개인들의 집단을 학력별로 비교하여 학력별로 평균 임금의 차이를 계산한 후, 그 차이들의 평균값을 구한다.
• 선형 인과모형 : Yi = α + ρ∙si + Xi'∙γ + vi
↪ si : 처치 (multiple case)
↪ Xi : 통제변수
↪ ρ : 인과효과
b. 누락변수 편의 공식
• omitted variable bias (OVB) 식은 서로 상이한 통제변수들을 갖는 모형에서 구한 회귀 추정치들 사이의 관계를 표현한다.
• 누락된 변수와 관심대상 변수가 서로 상관관계를 갖지 않는 경우, 짧은 모형 (독립변수가 적은 단순한 회귀모형) 과 긴 모형 (많은 수의 독립변수가 포함된 회귀모형) 의 회귀계수들은 언제나 서로 같다.
c. 부적절한 통제변수
• 설명변수들을 통제하면 회귀 추정치를 인과적으로 해석할 수 있는 가능성이 높아진다. 그러나 설명변수가 많아진다고 항상 좋아지는 것은 아니다. 어떤 변수들은 부적절한 통제변수들이므로 회귀모형에 포함되어서는 안된다.
③ 이분산성과 비선형성
• CIA 가 성립할 때 선형 인과모형은 인과적 해석이 가능한 선형 CEF 를 도출한다.
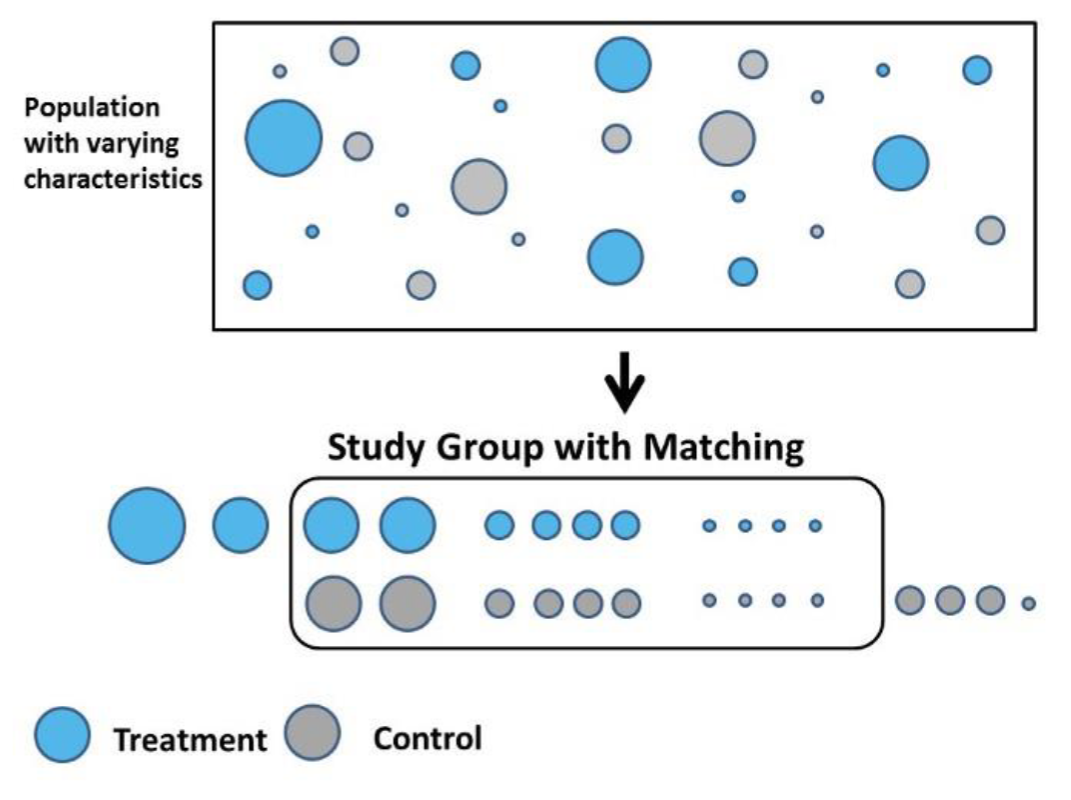
a. 회귀모형과 매칭
⇨ 처리 집단과 비처리 집단 중 한명씩 뽑아 비슷한 사람들을 매칭한다. 처리집단의 i 번째 데이터와 비처리 집단의 j 번째 데이터 간의 거리를 재서 ϵ 보다 작으면 (거리가 가까운 사람들끼리) 매칭된다. 이 pair 들에 대해 수치의 차이를 각각 구하고 평균을 취하면 Average treatment effect on the treated 를 구할 수 있게 된다.
v
• 설명변수를 통제하기 위한 전략으로 matching 은 회귀모형과 마찬가지로 CIA 에 기반을 둔 추정방법이다.
• 매칭은 각각의 설명변수 값에서 처치-통제 간 비교를 가능하게 하고 이렇게 구한 처치효과들을 가중평균하여 단일한 전체 평균 처치효과를 산출한다.
• 회귀모형의 경우 추정식은 모집단 회귀계수 벡터이다. 매칭 추정식은 일반적으로 처치집단과 통제집단 사이의 차이를 설명변수들에 의해 정의된 셀들을 이용해 가중평균한 값이다 ⇨ 관심 대상이 되는 모수는 처치를 받은 사람들에 대한 평균 처치효과 E(Y1i - Y0i | Di = 1) 이다.
• E(Y1i - Y0i | Di = 1)
↪ 직업훈련을 받은 사람들의 평균 임금 E(Y1i | Di =1) → 관측 가능한 수치
↪ 직업훈련을 받지 않았더라면 받게 될 가상적인 (counterfactual) 평균 임금 E(Y0i | Di=1) 간의 차이
• 처치된 사람들에 대한 처치효과를 추정할 때, 매칭은 처치된 사람들 사이의 설명변수의 분포를 가중치로 사용해 각 설명변수 값에 고유한 평균 효과들의 가중 평균을 구한다.
b. 성향점수를 이용해 설명변수를 통제하는 방법
• 관심대상인 원인변수가 처치 더미변수인 경우, 회귀모형 대신에 매칭을 사용하는 추정 전략 "propensity score theorem" 을 제안하였다.
• propensity score = P(Xi) = E(Di | Xi) = P(Di=1 | Xi) : 특정 개체가 치료군에 속할 확률, 다변량 설명변수 벡터 Xi (처치확률에 영향을 미치는 설명변수들만 통제하는 것으로 충분하다)

• p(xi) 를 구하는 방법
1) logit 이나 probit 같은 모수적 모형을 이용해 p(Xi) 를 추정한다 : 종속변수를 treatment 여부로 둔다.
2) 1단계에서 추정된 성향점수를 기준으로 매칭하여 처치효과의 추정치들을 계산한다.
⇨ 관찰 가능한 통제변수로 treatment 받을 확률을 모두 설명할 수 있다는 가정
c. 성향점수법과 회귀모형
• propensity score matching 은 E(Yi | Xi, Di) 추정으로부터 성향점수 P(Xi) = E(Di | Xi) 추저으로 전환시킨다.
• 회귀모형을 이용해 추정하기 전에, 성향점수를 사용해 체계적으로 표본을 선택해야 한다고 제안하고 있다.
'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| Hidden Markov Models in Marketing 노션 정리 (1) | 2024.12.14 |
|---|---|
| 계량경제학 스터디 Lecture 8. Regression Discontinuity (0) | 2023.05.25 |
| 계량경제학 강의_한치록_특수주제들 17장 (0) | 2023.05.25 |
| 계량경제학 강의_한치록_내생적인 설명변수 16장 (1) | 2023.05.24 |
| 계량경제학 강의_한치록_내생적인 설명변수 15장 (0) | 2023.05.24 |



댓글