👀 계량경제학 개인 공부용 포스트 글입니다.
1. Overview
① Outline
• Part1. Causality basics
↪ potential outcomes framework, randomized controlled trials, regression, matching
• Part2. Tools of Trade
↪ IV, DID, RD (regression discontinuity)
• Part3.Topics
↪ standard errors, robust estimation, ML and causal inference
• Importance of causal inference
• Potential outcomes framework
• Selection bias
• Randomization
• ATE
• Regression and treatment effect
② Objective
• Research question 에 있어 empirical study에 사용되는 계량경제학 방법이 왜 이상적인지 이해한다.
• 적절한 계량경제학 방법을 통한 실증적인 경제학 연구를 설계한다.
• 통계 소프트웨어를 활용한 다양한 실증모델을 통해 파라미터를 추정한다.
③ Causal inference vs Predictive models
• Input oriented approach : 원하는 output 에 달성하기 위해, input을 조작하거나 개입하는 것을 목적으로 한다면 인과추론 모델이 적합하다.
↪ EX. What is the cause of employment decreasing rates?
↪ EX. 추천시스템 : 사용자 B에게 물을 추천하는 것이 사용자 B가 물을 살 확률을 높입니까? 사용자 A와 B는 왜 비슷한 아이템을 구매합니까?
• Output oriented approach : 원하는 target 과 output을 비슷하게 만드는 것 (closest)을 목적으로 한다면 예측모델이 적합하다.
↪ EX. How can we prevent employment decreasing rates?
↪ EX. 추천시스템 : 사용자 B에게 물을 추천하면 추가 매출이 발생합니까?
④ Models

2. Causality
① Golden standard for causality
• Question : A가 B의 원인이 된다는 것을 어떻게 알아낼까
• 가장 이상적인 실험의 경우, 똑같은 agent 를 반복하여 하나는 treat를 가하고, 다른 것은 untreated 한 상태로 두는 것이다. 그러면 처치효과를 측정해 낼 수 있다.
• Cetris Paribus : 다른 모든 것이 같다 (all else being equal) ⇨ 실험의 신뢰성을 만드는 가정
• 인과효과를 밝힐 수 있는 잘 디자인된 실험을 고안해야 한다.
② Potential outcomes framework
• i : individual or economic agent
• treatment variable : Di = {0,1}
• Yi : outcome of interest
• question : Yi 가 Di 에 의해 영향을 받는지 여부
• 각 i 에 대해 2가지 잠재적 결과가 가능하다.

• treatment 의 인과효과 : Y1i - Y0i
✔ 'missing data problem' : 문제는 각 i 에 대해, Y1i와 Y0i를 동시에 관찰할 수 없다는 것! 따라서 observed outcome Yi에 대한 수식을 아래와 같이 정의할 수 있다.
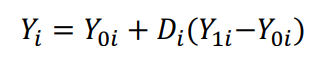
③ Selection bias
◯ missing data problem 을 해결하기 위해, treated person과 non-treated person의 결과를 비교해 볼 수 있다.

• Yi 를 개인 i의 건강지수라고 해보자. 입원 여부가 treatment 라고 했을 때 가령, 건강하지 않은 사람 K 가 입원을 한 경우의 건강지수가 4라고 하고 (Y1K = 4), 건강한 사람 M 이 입원을 하지 않은 경우의 건강지수를 5라고 하자 (Y0M = 5). 관측된 결과를 통해 우리는 hospitalization의 효과를 다음과 같이 계산할 수 있다 : (Y1k - Y0M = 4 - 5 = -1). 그러나 이러한 수치가 (Y1K - Y0K)를 대체한다고 말할 수 있을까. 건강하지 않은 K 사람과 건강한 M 사람을 비교하는 것은 hospitalization의 인과효과를 입증하기에는 부족하다. 아픈 사람이 입원을 하는 경우가 더 많은, 즉 Y0K < Y0M 이 된다는 것이다. 이는 treatment 이전의 상태가 다르다는 것을 의미하며 Cetris paribus 가정을 만족하지 못하게 된다. 즉, selection bias 가 존재하는 것이다.
• 수학적으로 다시 정의해보자면 Y0K (Counterfactual)를 더하고 빼는 부분을 추가하여,
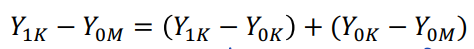
위와 같이 정의할 수 있고, 데이터에서 우리가 관찰할 수 있는 것은 Y1K - Y0M = 4 - 5 = -1에 해당 한다. 가설을 세워서 Y0K = 3 이라고 한다면 (Y1K-Y0K) = 4 - 3 = 1이라 할 수 있고 이는 K 라는 사람에 대한 입원이 건강지수에 미치는 인과효과에 해당한다. 더불어 (Y0K - Y0M) = 3 - 5 = -2 인 K와 M 사람이 입원하지 않을 때의 건강상태의 차이를 계산해낼 수 있다. 여기서 -2 는 K가 M 보다 덜 건강하다는 것을 의미한다.
◯ Selection bias
• treatment 이전에 두 sample 의 basline 이 다른 것
• Sample 이 모집단을 대표하지 못한다.
• treatment 가 없을 때에서의, treatment group (counterfactual) 과 control group 의 systematic 한 차이
• 사회과학적 연구에서, agent 는 처치를 받을지 말지에 대해 선택하기 때문에, selection bias 는 자연스럽게 발생하게 된다. selection bias 는 데이터의 크기와 관계없이 발생하는 문제이다.
• 두 개 이상의 관측치가 있을 때, 우리는 average treatment effect 를 추정해볼 수 있다.
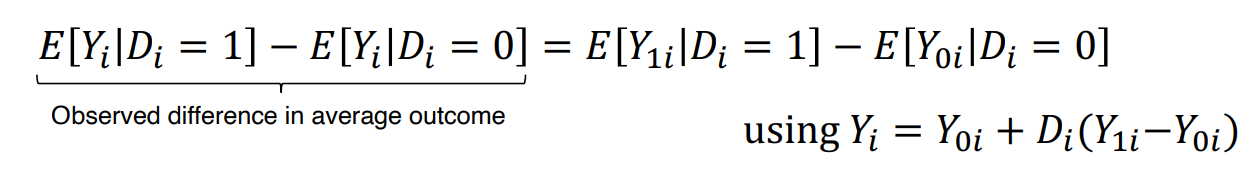
K 사람, M 사람의 예제와 같이 위의 식을 아래와 같이 재정의해볼 수 있다.

⇨ difference in group means = Average causal effect + selection bias
◯ ATT : average treatment effect on the treated
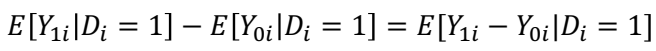
• ATT = 처치를 받은 것에 대한 처치의 평균 효과
• ATT ≠ ATE : ATE 는 E[Y1i - Y0i] 로 모집단으로부터 랜덤하게 선택된 unit 에 대한 기대효과를 의미하고, 전체 모집단에서의 평균적인 처치에 대해 다룬다. 반면 ATT 는 처치를 받은 집단에 대한 평균 처치효과에 대해 다룬다.
◯ Tackling Selection bias
• Selection bias 가 0이라는 것 E[Y0i | Di = 1] - E[Y0i | Di = 0] = 0의 의미 : 기저상태가 똑같다는 것, E[Y0i | Di = 1] = E[Y0i | Di = 0]
• [Y0i | Di = 1] 는 실제 관측할 수 있는 데이터가 아닌 hypothetical 한 부분이다.
• E[Y0i | Di = 1] = E[Y0i | Di = 0] 은 treatment 가 없을 때 처치 집단에서의 평균적인 잠재결과가 treatment 가 없을 때 통제 집단에서의 평균적인 잠재결과와 같다는 것을 의미한다.
• 쉽게 말하면, treatment 가 없을 때, 처치집단에서의 평균적인 결과는 통제집단에서의 평균적인 결과와 동일하다는 것이다.
④ Randomization
◯ 어떨 때 selection bias 가 없어질까
• Di 가 Yi 에 독립일 때, E[Y0i | Di = 1] = E[Y0i | Di = 0] 를 만족한다.
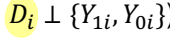
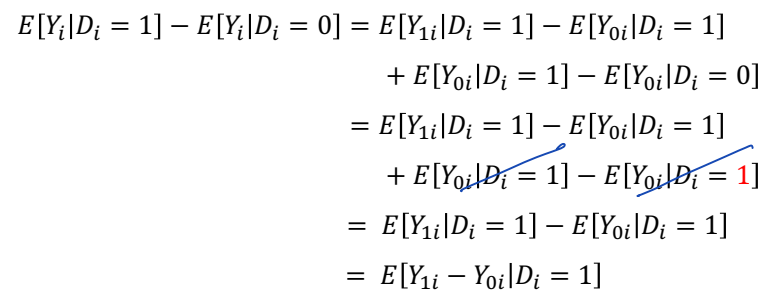
• 더불어 Di 와 Yi 가 독립이게 되면, randomized trial 에서 ATT 는 ATE 와 같아진다.
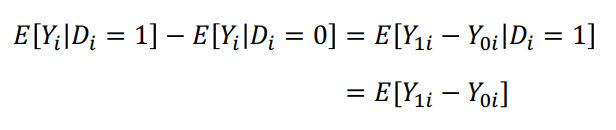
◯ 왜 랜덤화가 selection bias 를 없애는걸까
• 직관적으로 생각해보자. hospitalization 문제에서 selection bias 는 건강하지 않은 사람이 건강한 사람보다 입원할 가능성이 높아 treated 와 non-treated 사이에 systematic 한 차이를 만들어 selection bias 가 발생했었다. E[Y0i | Di = 1] < E[Y0i | Di = 0]
• 입원 결정을 동전던지기로 결정한다고 가정해보면, 큰수의 법칙에 따라 동전을 충분히 많이 던져볼 수 있고, 따라서 treated group 과 non-treated group 에서 건강한 사람과 건강하지 않은 사람의 비율을 같게 만들 수 있다.

↪ 왼쪽 테이블을 보면 입원한 사람 중에 unhealthy 한 사람의 비율은 70% 에 해당하고, 입원하지 않은 사람중에 healthy 한 사람은 70%에 해당한다. 즉, selection bias 가 존재하는 상황이다.
↪ 반면, 오른쪽과 같이 randomization 을 적용한 결과에서는 각 group 에서 건강한 사람과 건강하지 않은 사람의 결과 비율이 동일하기 때문에 (※ cell 에 있는 수치는 Yi 를 의미하는 것이 아님. 관측한 case 의 개수를 의미함. 관측치 수) selection bias 가 없는 상태에 해당한다.
• E[Y0i | Di = 1] = E[Y0i | Di = 0] : pre-treatment outcome 이 처치집단과 통제집단에서 동일하다. 즉, 입원하기 전 (treatment 가 가해지기 전)에, 처치집단에서의 health condition 은 통제집단에서의 health condition 과 동일하다고 볼 수 있다.
◯ 정리
※ 처치집단 = (처치받을 집단, 처치받은 집단), 통제집단

• [Y1i | Di = 1] : 처치받은 처치집단 (post-treatment outcome)
• [Y0i | Di = 0] : 처치받지 않는 통제집단
• [Y0i | Di = 1] : 처치받을 처치집단 (아직 treatment 를 가하지 않은 상태 : pre-treatment outcome) → 그러나 동일한 i 내에서 pre-treatment 인 상태를 관측하기 어렵다. 그래서 이를 [Y0i | Di = 0] 로 대체해서 ATE 를 계산하려고 하는 것인데, treatment group 에 (ex. K사람) 대응하는 control group 을 (ex. M사람) 선택하는데, 있어 treatment 이전의 기저상태가 다르다는 selection bias 가 존재하는 것이다. 따라서 이를 해결하기 위해 Randomization 을 실행할 수 있다.
◯ Random assigned treatment 와 동의어
• Exogenous treatment
• Unconfoundedness
• Ignorability : missing data 문제를 무시해도 괜찮다.
◯ Randomization in Practice
• 실무에서는randomization 이 A/B test 라고 알려져있다.
• A/B test 는 A와 B 두 변수에 대한 랜덤화된 실험으로 구성되어 있다.
• Pros : selection bias 를 통제 가능하고, 외생변수로부터의 악영향을 보다 효율적을 관리할 수 있고 (internal validity), 반복 가능하다.
• Cons : 인위적으로 조작할 가능성이 높고, 일반화가 어려우며, 비용이 많이 들고, 윤리적인 한계점이 존재한다.
• 표준 실험 과정

◯ Experiment evaluation
• Internal validity
↪ 인과적 관계가 존재하는가, 독립변수가 종속변수의 변화에 단독적으로 인과효과를 미치는가
• External validity
↪ 실험의 결과가 실제 세계에 적용이 가능한가 (population validity)
↪ 일반화가 가능한 결과의 수준인가 (ecological validity) : 실험 과정에서 수많은 노이즈가 포함될 수 있다.
• Threats to External validity
↪ Hawthorne effect : 실험 참가자들이 실험에 참가하고 있음을 인지하는 것으로부터 오는 효과
↪ placebo effect
↪ Multiple treatment interference
⑤ Regression and Treatment effect
• 주어진 데이터에서 treatment effect 는 표본 평균 (sample averages) 을 비교함으로써 추정해볼 수 있다. 이는 Di 에 대한 Yi 의 회귀분석을 통해 투정할 수 있다.
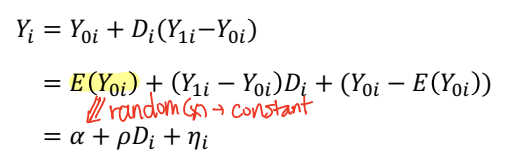
↪ Di = 0 인 경우 : Yi = Y0i
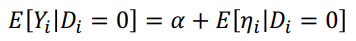
↪ Di = 1 인 경우 : Yi = Y1i
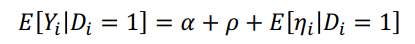
↪ α = E(Y0i) : constant
↪ ρ = (Y1i - Y0i) : treatment effect
↪ η = Y0i - E(Y0i) : error
• Di 에 대한 Yi 의 회귀분석을 통해 α 와 ρ 를 추정한다. E(ηi) = 0.
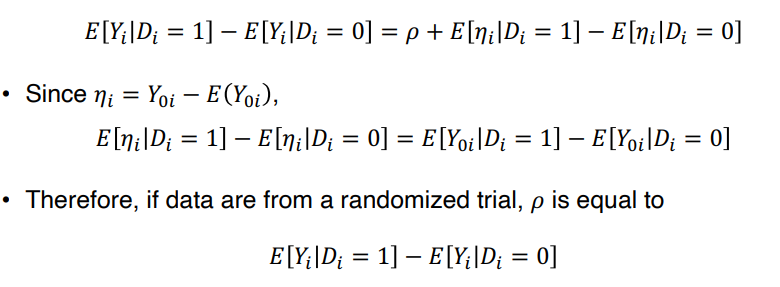
3. Paper example
◯ Paper Formation

◯ Research Question and Motivation
• 재택근무는 흔한 사례가 되었다. 특히 코로나19 이후 더 흔한 업무방식이 되었다.
• 재택근무가 생산성과 수익성을 증가시키는 유용한 역할을 하는가 : 통근시간을 줄임으로써 업무 효율성을 높일 수 있다, 그러나 매니저들은 직원이 집에서 일하게 되면 shirking (해고) 사례가 증가할 수 있음을 걱정한다.
◯ Research Design
• Experiment
↪ 상하이 콜센터 (출발지의 항공숙박 예약 회사) 직원들을 대상으로 실험
↪ 집에서 일주일에 4교대(일)를 일하고, 회사가 정한 요일에 사무실에서 5교대를 일하는 것을 treatment 로 설정 (재택근무가 직원들의 생산성과 수익성에 미치는 효과)
↪ control 집단은 5일 모두 9시부터 5시까지 오피스에서 일하는 사람들로 설정
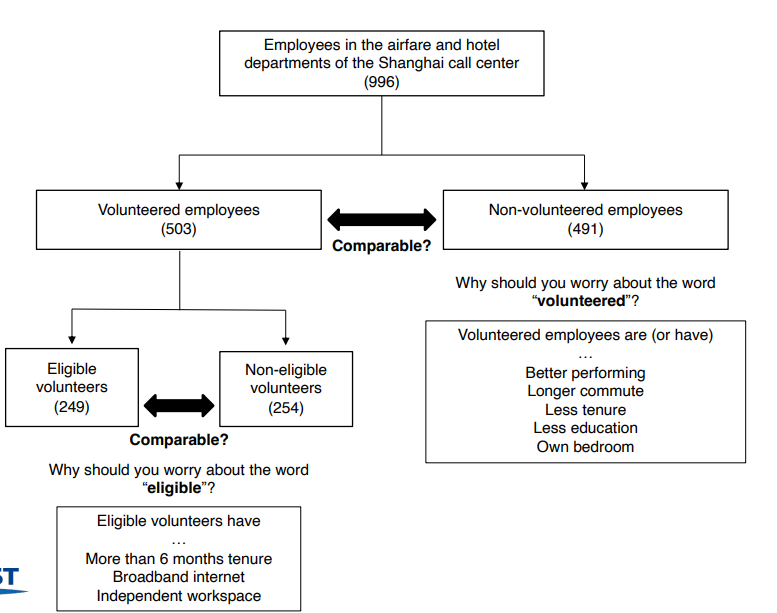
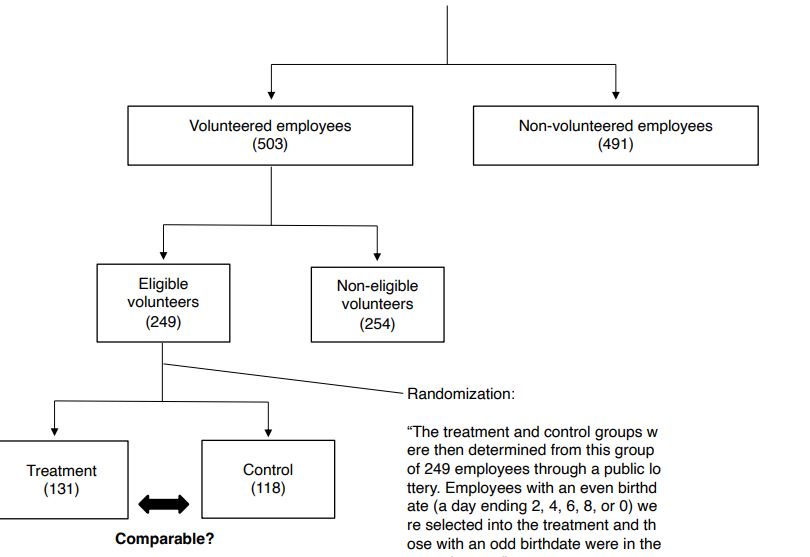
• Treatment group 와 control group 사이에 차이점이 무엇이 있을까
↪ 처치집단은 전화응대에 들이는 시간이 적음
↪ 처치집단에 속한 근무자는 상급자로부터 받는 support 가 상대적으로 적음
↪ 근무환경이 다르다는 점 : 처치집단은 조용한 환경에서 혼자 일하는 경우가 많다.
◯ Data
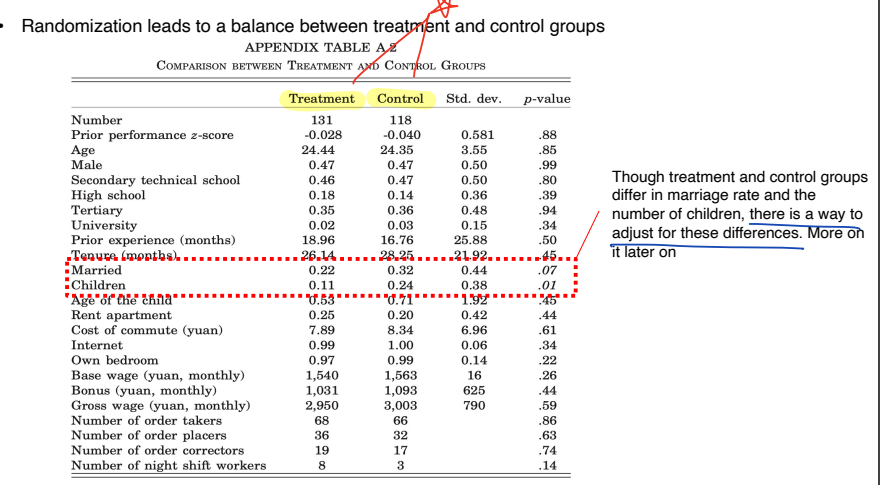
• 데이터에서 단순히 통계수치만 확인하지 말고, 설정한 가설이 데이터에 통용되는지 살펴보아야 한다.
• 대부분의 수치에서 treatment 와 control group 이 비슷한 결과를 보여주고 있으나, Married 와 Children 속성에 관해서는 0.1 정도의 차이가 발생하고 있다. 이러한 차이를 조정할 수 있는 방법이 필요하다.
◯ Results
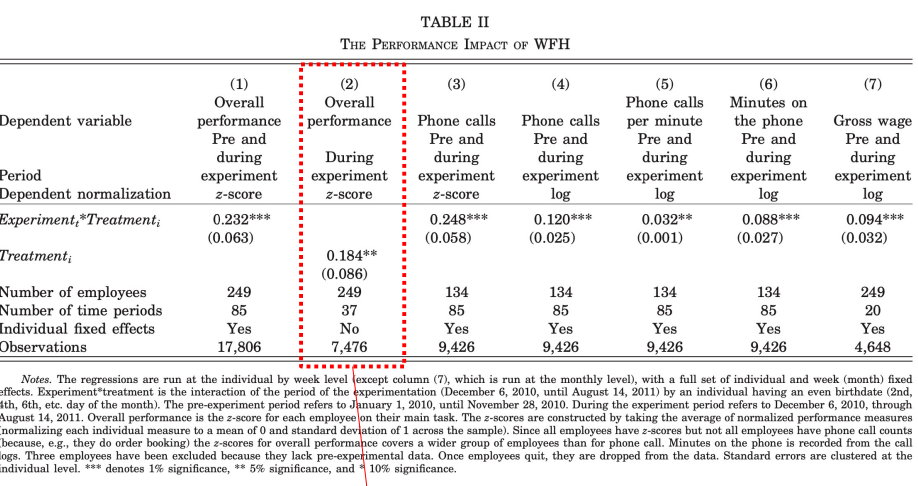
• treatment group 에서의 전체 업무 성과 (overall performance) 를 살펴보면, control group 보다 standard deviation 이 0.184 정도 높음 (데이터의 분포가 넓게 퍼져 있다는 것을 나타내며, 데이터가 상대적으로 더 다양한 값을 가지고 있다는 것을 의미) 을 볼 수 있다.
• 좋은 논문은 주요 질문 (ex. 재택근무가 생산성과 수익성을 증가시키는가) 을 다룬 뒤에 mechanism 을 파해친다. 가령 위의 예제에서는, 재택근무가 교통이 나쁘거나 눈이 많이오는 날에 대한 영향을 피할 수 있어 더 철저하게 일을 시작할 수 있었으며 병원 등 개인 일정을 스케쥴링 할 수 있고, 점심이나 화장실을 집에서는 빠르게 해결할 수 있어 쉬는 시간이 더 짧아졌다는 mechanism 을 도출했다.
◯ Summary & Discussion
• Concern1 : Potential Hawthorne and Gift-Exchange Effects : 직원들이 실험에 동기부여를 받아 고의적으로 회사가 재택근무를 계속 유지하도록 행동했을 수 있다 → 추후 실험에서는 survey 를 진행하여 이를 해결했다.
• Concern2 : Attrition : 대조군에서 성과가 저조한 직원은 치료군에서 근무하는 직원보다 퇴사할 가능성이 높았다. 따라서 대조군에 있는 다른 직원들이 감정적인 영향을 받았을 수도 있기 때문에 재택근무의 영향을 추정한다고 보기 어려울 수 있다 → 해당 문제는 control group 을 실험기간 전체동안에는 그만두지 않게 하도록 하여 해결할 수 있다.
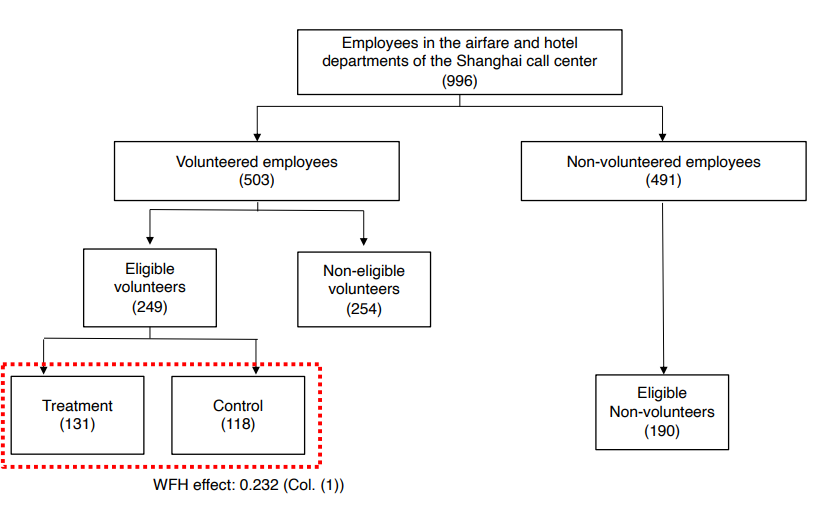
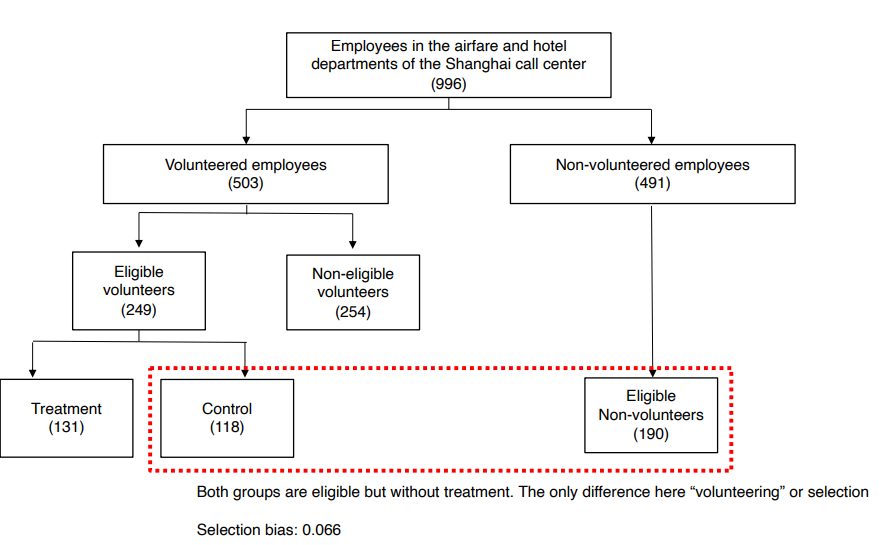
• Concern3 : External validity : 재택근무를 자진지원한 사람들은 재택근무 참여를 선택할 수 있다는 점을 주목해야 한다. 보통 지원자들은 성과를 잘 내는 직원들일 수 있다. 재택근무를 하지 않더라도 성과를 잘내는 사람들일 수 있다는 selection bias 가 존재한다.
• Selection bias 를 다루는 방법
'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| R 강좌 : 정책효과 분석 : 이중차분법 DiD, 삼중차분법 DDD (0) | 2023.05.09 |
|---|---|
| 계량경제학 강의_한치록_단순회귀 1장~2.4장 (0) | 2023.05.09 |
| 계량경제학 스터디 CH11,12,13,14,15정리 (0) | 2023.04.09 |
| Difference-in-Difference (DiD) (0) | 2023.04.03 |
| 계량경제학 스터디 CH7,8,9,10정리 (0) | 2023.03.31 |



댓글