👀 계량경제학 개인 공부용 포스트 글 입니다.
CH11. Endogeneity and Instrumental variables estimation
① Linear Regression with the random regressors
• E(ei | xi) = 0 의 의미는 같은말로 Cov(e,x) = 0 : e 와 x의 공분산이 0 (상관관계가 없다)

• 내생성과 외생성

↪ 내생성 : x 와 e 가 상관관계가 있다.
↪ 외생성 : x와 e 가 상관관계가 없다. E(xe) = 0
② When x and e are correlated (the case of endogeneity)
• x와 e가 연관되어있을 때 : 내생성
• 예시1. 내생성


• 예시2. 외생성

• 예시3. 내생성

• 예시4. 내생성 : simultaneity

• 외생성 조건이 깨지는 경우
⇨ 1. Omitted variable 변수 누락

누락된 변수로 인해, Cov(x,u) 가 0이 되지 않으며 내생성이 발생한다.
⇨ 2. Measurement errors 측정오차

측정오차로 인해, Cov(x,u) 가 0이 아니게 되며, OLS estimator b2 또한 biased (inconsistent) 된다.
⇨ 3. Lagged dependent variables model (time series)
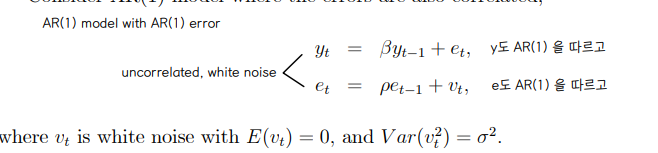

③ IV estimation
• E(xe) 가 0이 아닐때, bias 없이 어떻게 β를 estimation 할까 ⇨ e 와 correlation 이 없는 외생변수 z 를 찾아보자 ⇨ z 는 instrumental variable

• 도구변수 조건
↪ 1. E(ze) = 0 : e 와 correlation 이 없다.
↪ 2. Corr(z,x) as high as possible : x와 z의 상관성은 높다.
• 도구변수로 구한 β estimation : IV estimator


④ Two-stage LS estimator
• IV 가 하나의 regressor 에 대해 다수로 존재할 수 있다. 도구변수는 많을수록 좋다.
• 도구변수 생성 방법
↪ 횡단면 자료 : Cov(z,e) = 0 , Cov(x,z) >> 0
↪ 시계열 자료 : 주로 X Lag 를 많이 사용한다. (Xt, Xt-1, ...)
[1단계] 외생적인 요인 추출 : regressor 에 대하여 외생변수 (k개) 에 대해 회귀분석을 돌려 내생변수를 만든다.
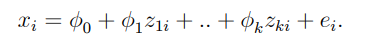

[2단계] exogenous components 에 대한 y 의 회귀분석을 진행한다. x^ 은 z에 대한 정보만을 포함하고 있으며, v 와 상관관계가 없다.

• example 1

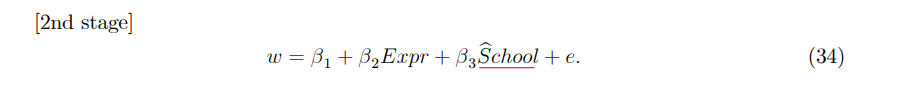
• example 2

• example 3

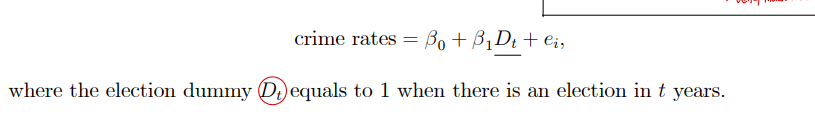
• 시계열 자료에서의 도구변수

⑤ Efficiency of IV estimator
• 도구변수를 사용했을 때의 estimator 의 분산은, OLS 의 estimator 분산보다 항상 크다. 즉, b_IV 가 덜 효율적이다.
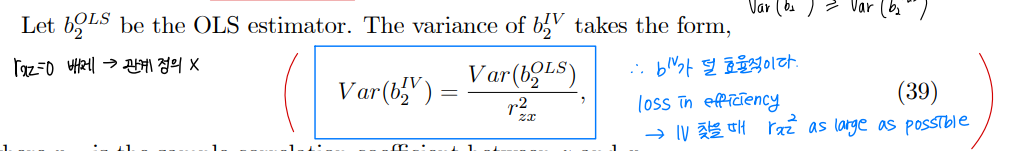

• 도구변수가 x 변수와 강한 상관관계를 가질 때, strong IV 라고 부른다.
• 도구변수가 strong 한지 weak 한지 t-test (for one IV) 혹은 F-test (for multiple IVs) 한지를 검정할 수 있다.
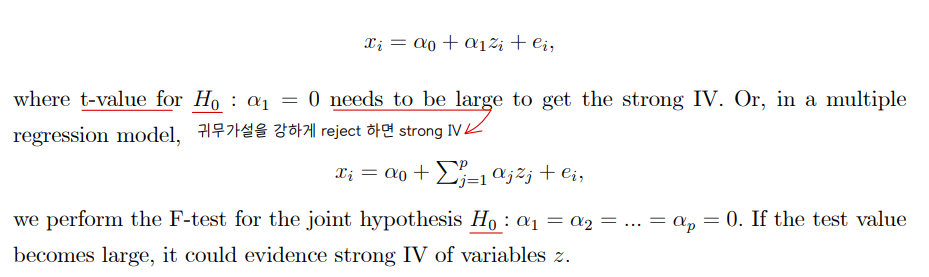
CH12. Volatility ARCH models
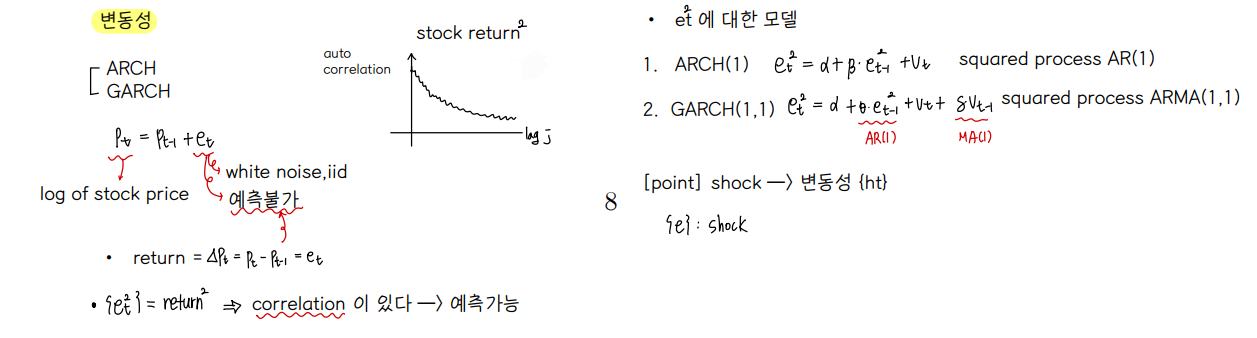
① ARCH
• AutoRegressive Conditional Heteroskedasticity 시차를 가지는 조건부 이분산성
• Volatility = 변동성 = 분산 : 금융경제학에서 매우 중요한 지표 중 하나다. 시계열에서 변동성을 예측하는 것에 관해 다룬다.
• shock (충격) e 는 unpredictable 하다. 따라서 우리는 e의 분산을 예측하는데 집중한다.

• Volatility 는 다양한 방식으로 모델링 될 수 있는데, 여기서는 ARCH 모델에 대해 배워보려고 한다.

• ARCH

↪ error 에 대한 가정들 : E(et) = 0 , E(et∙e_t-j) = 0, 동분산성, E(et | I_t-1) = 0 예측불가능성, E(et^2 | I_t-1) = ht
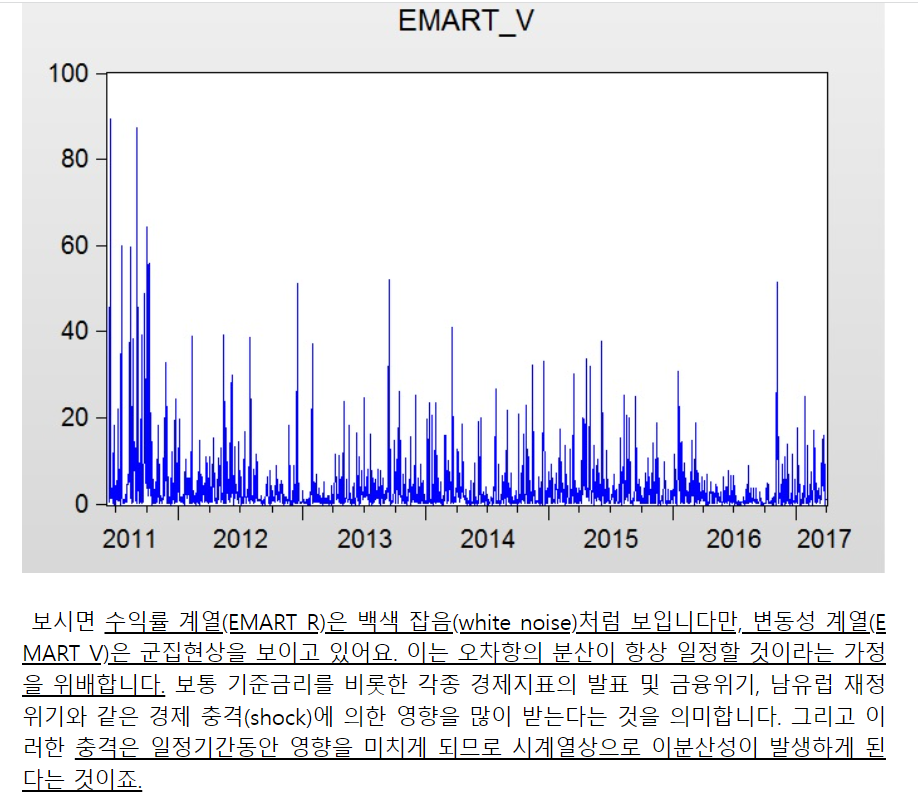
↪ Volatility Clustering 군집현상
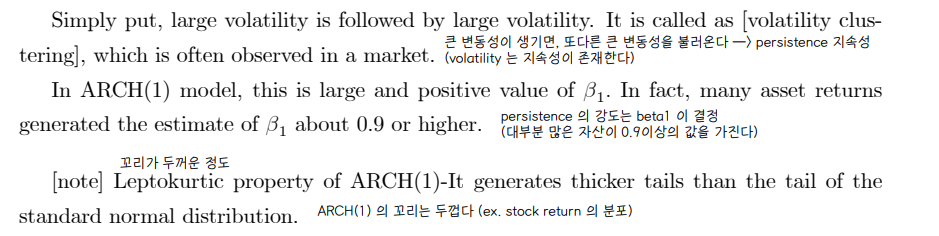
② ARCH(1) process equals to AR(1) process for squared errors


• ARCH(1) 모델은 AR(1) 모델로 작성해볼 수 있다.
③ Testing for ARCH
• ARCH 를 만드는 term 이 존재하는지 안하는지에 대한 검정

④ GARCH
• Generalized ARCH

• Summary
CH13. Multiple time series and VAR (Vector Autoregression) models
다변수 시계열, AR 을 vector 로 확장 Vector auto regression

① Structural and reduced from models

• x와 y 의 2개의 시계열 변수
• SF : structural form

x 와 y 변수를 벡터형태로 표현한 Zt 변수에 대해 풀어서 적으면 AR(1) form 을 만족한다.
VAR form 에서 error ut 는 correlated 되어있다.

• structural model 에서 미지수의 개수



② Estimating VAR model and Impulse response analysis
• VAR(1)
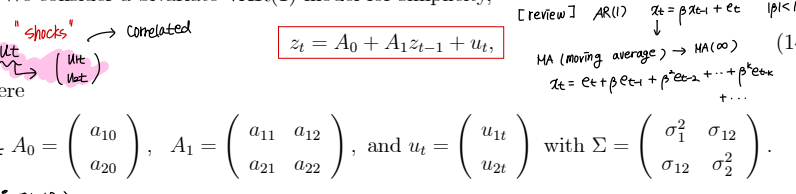
• 충격반응분석 : 모형으로부터 도출된 이동평균모형으로 경제에 예상치 못한 변화 (충격) 이 주어졌을 때, 모형내 모든 변수들이 시간의 흐름에 따라 어떻게 각 충격에 반응하는가를 나타내주는 것. 간단하게 얘기하면 한 변수에 충격이 가해졌을 때, 다른 변수들에 어떠한 영향이 있는지를 살펴보는 분석이다.


⇨ 충격반응 분석이 의미있으려면, 충격들 사이에 상관관계가 없어야 한다. 즉, Ut 를 서로 uncorrelated 하게 만들어야 한다 ⇨ Cholesky Decompositions:
• Cholesky Decompositions : Steps to obtain orthogonalized(uncorrelated) shocks


• 촐레스키 분해 이후 충격반응 분석

③ Application of VAR model : Granger-Causality
• 인과관계보단, 예측의 의미로 봐야한다.
• y의 영향은 없다. y does not G-cause over x



• Granger-Causality between the two series

CH14. Regression with Panel data
① Introduction
• 패널 데이터를 사용하는 이유 : 모형 설정 차원에서 관측되지 않는 이질성을 살펴볼 수 있다. 변수누락편향을 줄일 수 있다.
• 패널 데이터



패널 모델을 사용하여, 관측되지 않는 영향을 제거하여 unbiased 된 estimator 를 구할 수 있다.
② Unobserved heterogeneity and Fixed Effects panel model
• example of panel data
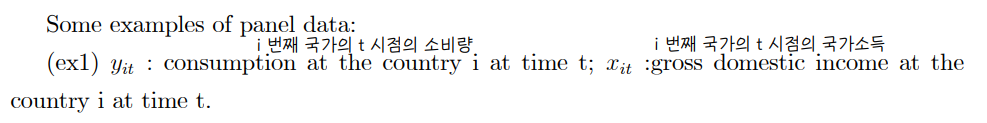

• Panel model

• Fixed effects or Random effects
αi 부분을 어떻게 접근할 것인지에 따라 Panel 모델은 2가지로 나뉠 수 있다.

• FE model

• RE model

• FE model 을 선택해야 할까 RE model 을 선택해야 할까
(ex1). 임금과 사원연수

(ex2). 특허권과 연구개발비용

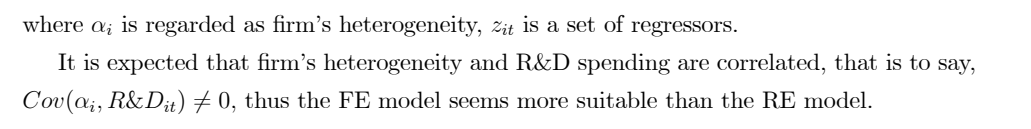
(ex3). 고속도로 차사고 사망률

• Estimation 방법
(1) First-Difference Approach : 서로 다른 t 시점의 값을 이용해, 차분을 통해 α 부분을 제거한다.


(2) Demeaned Regression : 원래 값과, 평균 값의 차분을 통해 α 를 제거한다.

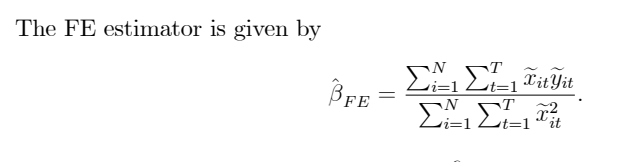
③ Random effects model
• RE 모델의 경우, 이분산성이 발생하기 때문에 OLS estimate 가 아닌 GLS 로 추정을 진행해야 한다.

④ Specification Tests : Hausman test

• 따라서 Cov 를 직접 구하기 보단, FE 의 beta 추정값과 RE 의 beta 추정값의 차이를 기준으로 가설검정을 진행한다.
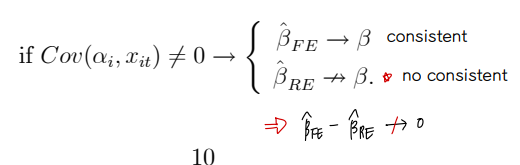

⑤ Time Effects Model
• 시간효과 : 시간에 따라서만 변하는 변수가 있을 수 있음 → demeaned model 로 관측불가능한 해당 변수를 제거


⑥ IV estimations in panel models
• 내생성 문제를 패널 모델에 적용해볼 수 있다.


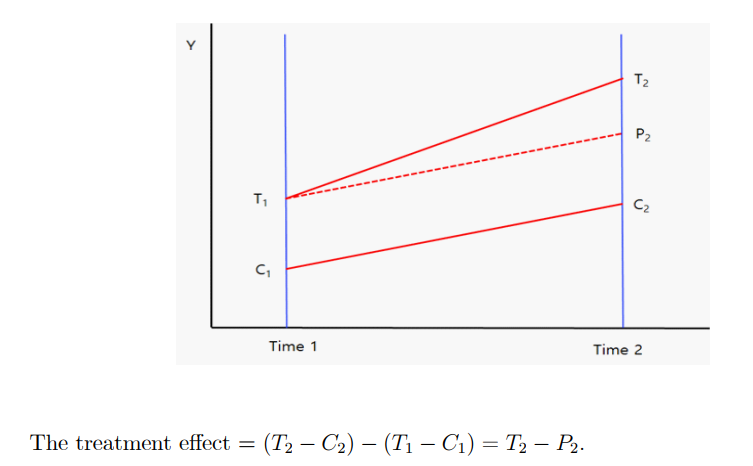
⑦ Policy analysis using panel data
• DID model → using panel data
CH15. Models with discrete choice variables
① Binary Choice Models

• 조건부 평균은 조건부 확률값이 된다.
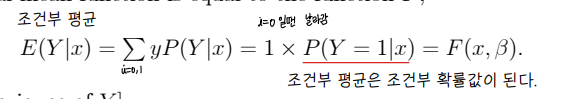
• 이때 F function 은 선형으로 모델링 하면 안된다 ⇨ Probit model 을 사용하여 F 결과를 0~1사이의 값으로 나오도록 해야 한다.
② Probit model
• 누적분포함수 cdf 를 사용해 F(x,β) 를 0과 1사이의 값이 나오는 함수가 되도록 모델링 한다.

'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 강의_한치록_단순회귀 1장~2.4장 (0) | 2023.05.09 |
|---|---|
| 계량경제학 스터디 Lecture 1. Introduction (0) | 2023.05.08 |
| Difference-in-Difference (DiD) (0) | 2023.04.03 |
| 계량경제학 스터디 CH7,8,9,10정리 (0) | 2023.03.31 |
| 계량경제학 스터디 CH3,4,5,6 정리 (0) | 2023.03.19 |



댓글