※ 참고링크
① HMM - Part2 (Decoding)
◯ Decoding Problem → HMM 의 핵심
▢ Decoding 문제 정의
• Problem : HMM(λ*) 과 O 가 주어졌을 때, 최적의 S 를 찾는 것 (가장 그럴싸한 은닉상태의 시퀀스 결정)
• Solution : Viterbi algorithm
• ex. 정 박사가 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑했다면, 각 날들 날씨는 ?

▢ Viterbi algorithm
• vt(i) : t 번째 시점의 i 은닉상태의 확률
[t=1 에서의 계산]

• v1(1) = (S1이 t=1에서 발생할 확률) • (S1 은닉상태에서 산책이 관찰될 확률) = π1•b1(산책)
• v1(2) = (S2가 t=1에서 발생할 확률) • (S2 은닉상태에서 산책이 관찰될 확률) = π2•b2(산책)
[t=2 에서의 계산]
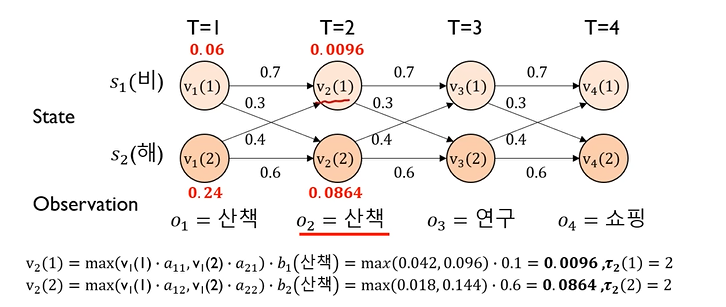
• v2(1) = max( v1(1) • a11, v1(2) • a21 ) • b1(산책)
• v2(2) = max( v1(1) • a12, v1(2) • a22 ) • b2(산책)
↪ max : 비 상태에서 올 확률과 해 상태에서 올 확률 중 큰 확률을 선택
[t=3 에서의 계산]

• v3(1) = max( v2(1) • a11, v2(2) • a21 ) • b1(연구)
• v3(2) = max( v2(1) • a12, v2(2) • a22 ) • b2(연구)
[t=4 에서의 계산]
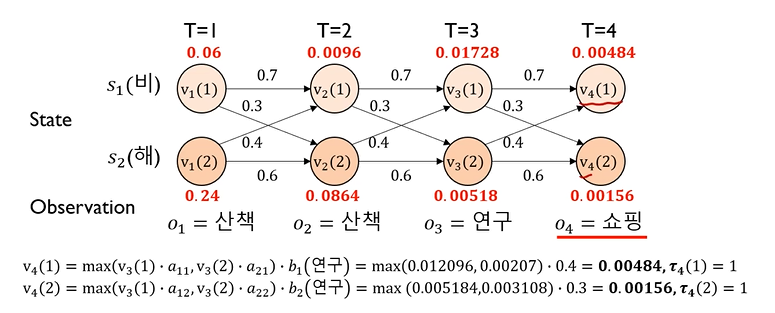
• v4(1) = max( v3(1) • a11, v3(2) • a21 ) • b1(연구)
• v4(2) = max( v3(1) • a12, v3(2) • a22 ) • b2(연구)
👀 Evalution 의 forward 알고리즘에서는, observable sequence 의 확률을 구하고 싶기 때문에 SUM 을 하는 전략을 선택했으나, Decoding 의 Viterbi 알고리즘에서는, 그 관측치에서 가장 그럴싸한 hidden state 를 찾아야 하기 때문에 Maximum 을 취함
👀 계산은 바로 이전 시점의 정보만 활용하기 때문에 computationally efficient 하다. 그러나 정보가 축적되어 전달되기 때문에 모든 정보를 사용하는 꼴이 된다.
[최종 hidden state 예측]
• 각 time 별로 구한 확률 중에 큰 값의 상태를 선택 : ex. T=1 시점에는 0.24 > 0.06 이니까 "해" 상태를 선택

• Qt_hat : 가장 최적의 hidden state sequence
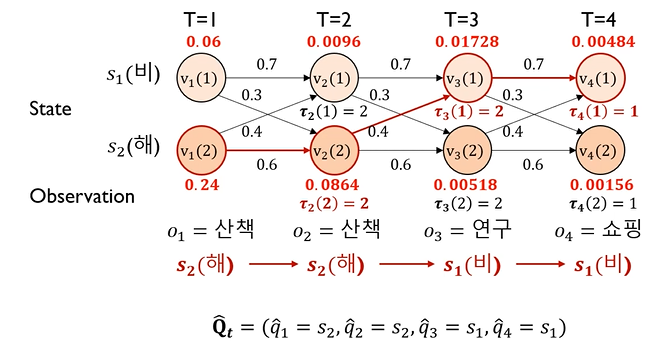
◯ Viterbi algorithm
▢ 수식 정리
• 앞의 예제를 통해 설명한 부분을 수식으로 정리하면 아래와 같음

▢ Evaluation vs Decoding
• Forward 알고리즘은 가능한 모든 경우의 확률의 합으로 Observable sequence 의 발생 확률을 구했고, Vitebi 알고리즘은 가능한 모든 확률중 가장 큰 값을 선택함으로써 가장 그럴싸한 hidden state 를 선택한다.

② HMM - Part2 (Learning)
◯ Learning problem (학습)
▢ Parameter learning
• 관측벡터 O 의 확률을 최대로 하는 HMM(λ) (파라미터) 을 찾자
• 여러 개의 관측 시퀀스를 줄테니 최적의 HMM 파라미터를 찾자
• Training data O 가 있을 때 λ 를 찾는 것

▢ Procedure of HMM Learning
• input : HMM(λ) architecture
• output : HMM(λ*) = {A*, B*, π*} → Optimal 한 parameter 구하기
• Algorithm
⑴ HMM 초기화 : 파라미터 초기화
⑵ 적절한 방법으로 P(HMM(λ_new)) > P(O | HMM(λ)) 을 찾아라 : 좋은 방향으로 이동
⑶ 만족스러우면 λ_hat = HMM (λ_new) 로 설정하고 멈춤 혹은 ⑵ 반복
◯ Baum-Welch algorithm
▢ 바움-웰치 알고리즘
• Problem : X={O1, ... , ON} 이 주어졌을 때, HMM(λ*)
• Solution : Baum-Welch 알고리즘 (or forward-backward 알고리즘)
↪ EM 알고리즘에 속함 (Estimation - Maximization)

↪ ϒ 와 ξ를 구하고 λ 를 구하고, 구한 λ 로 ϒ 와 ξ를 구하고, 구한 ϒ 와 ξ를 가지고 λ 를 구하고 ∙∙∙
▢ E-step

※ α : forward probability , β : backward probability
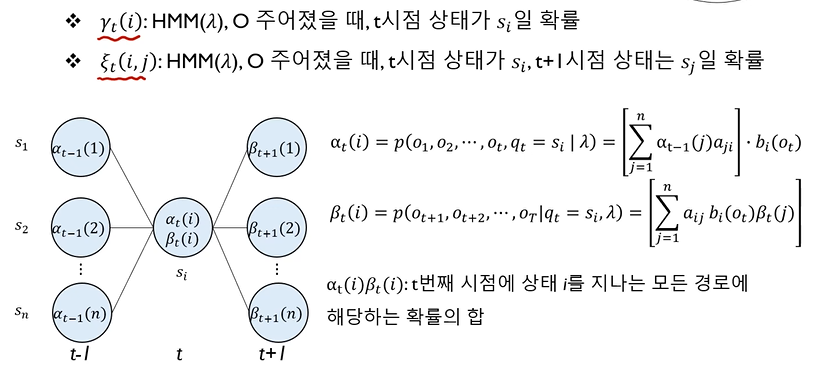
• ϒt(i) : HMM(λ), O 가 주어졌을 때, t 시점 상태가 si (hidden state 가 i) 일 확률

↪ 분자 : αt(i)•βt(i) : t 시점에서 si 일 확률
↪ 분모 : S1,S2, ... , Sn 일 확률을 모두 더한 값 (n : hidden state 의 종류 개수)
• ξt(i, j) : HMM(λ), O 가 주어졌을 때, t 시점 상태가 si, t+1 시점 상태는 sj 일 확률
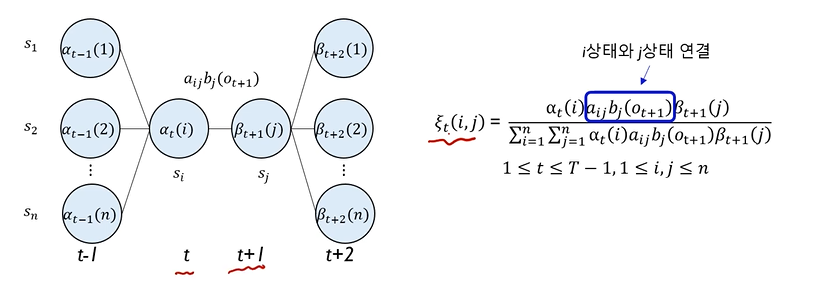
↪ i 상태와 j 상태를 연결해주는 계산값이 추가되는 형태
▢ M-step
• E-step 은 α , β 를 계산하여 ϒt(i), ξt(i, j) 를 구하는 것
• M-step 은 ϒt(i), ξt(i, j) 를 이용하여 HMM(λ) 를 개선 → HMM(λ_new)
↪ 개선 : P(HMM(λ_new)) > P(O | HMM(λ)) → 즉, HMM(λ_new) 의 evaluation 시 높은 확률

• πi_new : t=1 (시작시점) 일 때 si 에 있을 확률 ⇨ ϒt=1(i) , 1 ⩽ i ⩽ n
↪ Expected number of times (전체에서 몇번 발생하는지로 추정) in state si at time t=1
↪ Counting 으로 estimation

• αij_new : (si 에서 sj 로 전이할 기대값) / (si 에서 전이할 기대값)
↪ ϒt 와 ξt 를 사용해서 계산

• bi(vk)_new : (si 에서 vk 를 관측할 확률) / (si 에 있을 확률) = (i 상태 하에서 관측치가 vk 일 확률) / (i 상태가 나타날 확률)
↪ ϒt 를 사용해서 계산

• 파라미터 업데이트 정리
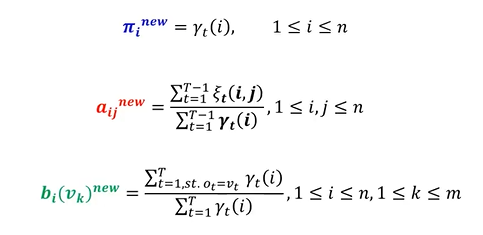
▢ E-M step
• (1) 에서 임의의 A,B,π 로 ξ,ϒ 를 구함
• ξ,ϒ 로 새로운 A,B, π 를 구함
위 두 과정을 반복 ← 확률이 커질때까지 반복

• "만족스러울 때까지" 반복 - "만족" 의 의미
↪ a. 업데이트된 경우에서의 확률과 이전 경우에서의 확률의 차이가 특정 값 이하인 경우
↪ b. 업데이트된 경우에서의 확률이 특정 값 이상인 경우
• 알고리즘

③ HMM 응용
◯ [HMM Evaluation Application] 제조공정 저수율 설비 경로 탐지
• 관측 시퀀스 : 설비 ID 데이터 (ex. 설비1, 설비4 ∙∙∙)
• 은닉 시퀀스 : 공정 ID 데이터
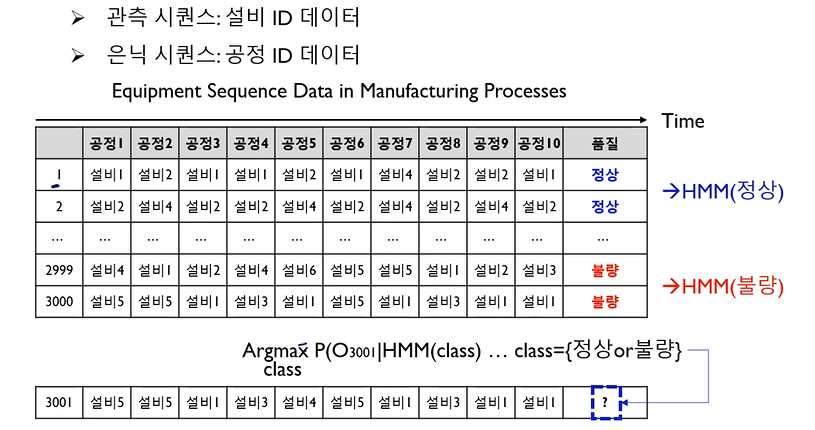
• 정상 제품만 가지고 HMM 모델을 만들고, 불량 제품만 가지고 HMM 모델을 만들 수 있음
• 미래에 3001번 제품이 들어왔는데, 관측 시퀀스가 있을 때, 정상일지 불량일지 알고싶음
↪ observable sequence 를 HMM(정상) 모델에 넣었을 때 P(정상) 정상일 확률이 나오고, HMM(불량) 모델에 넣었을 때 P(불량) 불량일 확률이 나오게 됨 ⇢ P(정상) 인 확률이 P(불량) 일 확률보다 크면 정상으로 분류
◯ [HMM Decoding Application] Sleep Quality Evaluation
• 관측 시퀀스 : 수면 EEG 데이터
• 은닉 시퀀스 : REM-수면, NREM-수면, Wake
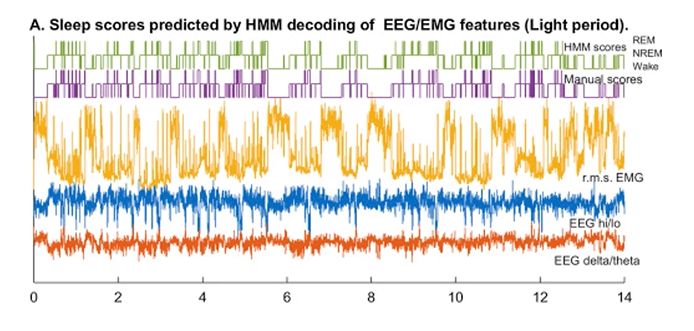
• 어느 부분이 램수면 상태이고, 램수면아닌 상태이고, 깨어있는 상태인지 3가지 hidden state 중에 예측
'1️⃣ AI•DS > 📙 Model' 카테고리의 다른 글
| HMM 기본 코드/응용사례 정리 (0) | 2024.01.05 |
|---|---|
| HMM 기초 개념 정리 - ① 개념, Evaluation (1) | 2024.01.03 |
| Tabnet (0) | 2022.03.31 |



댓글