※ 참고링크
① HMM - Part1 (개념)
◯ 순차 데이터
• 시간에 따라 얻어지는 데이터
• 시간성 특성이 있음

• 예시

↪ 하나의 제품이 완성품이 될 때까지는 10개의 공정을 거치고, 각 공정별로 여러 설비 종류를 가지고 있음
↪ 공정을 거치는 것을 시간의 흐름으로 볼 수 있음
• 순차 데이터 인식 예시

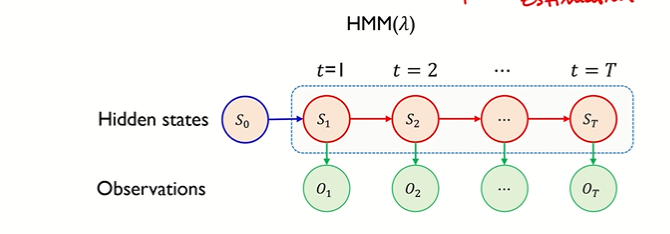
◯ Hidden Markove Model (HMM)
• 순차 데이터를 확률적 (Stochasic) 으로 모델링 하는 생성 모델 (Generative model)

◯ Markove Model 이란
• state 로 이루어진 sequence 를 상태 전이 확률 행렬로 표현하는 것

• 상태 전이 확률 행렬 : 상태가 변화하는 것을 확률로 표현
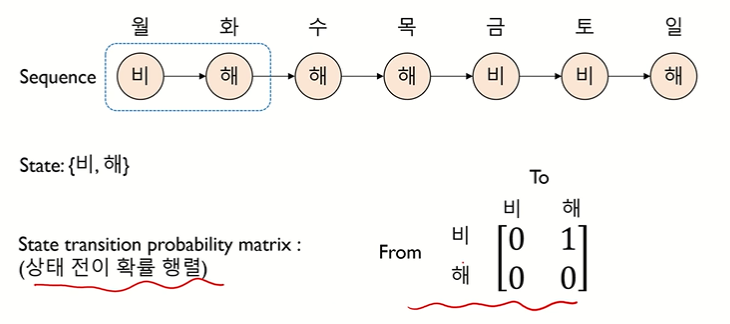
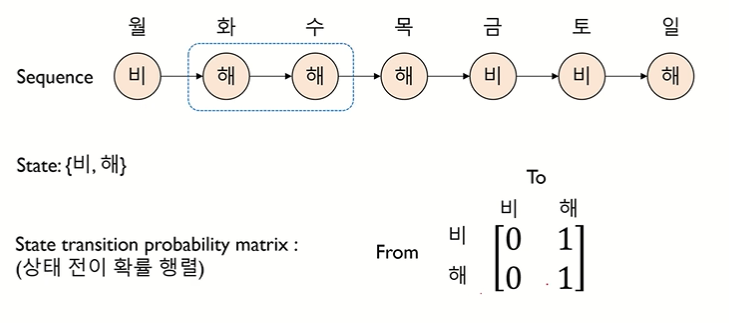
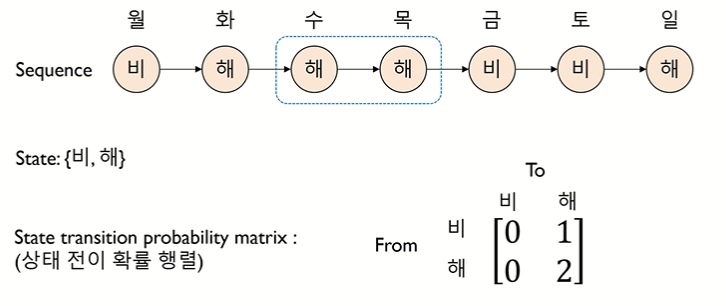
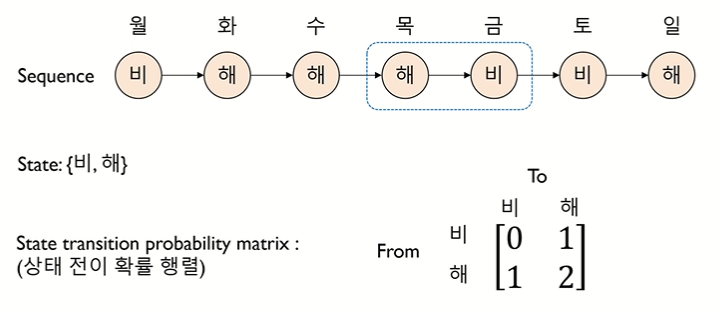
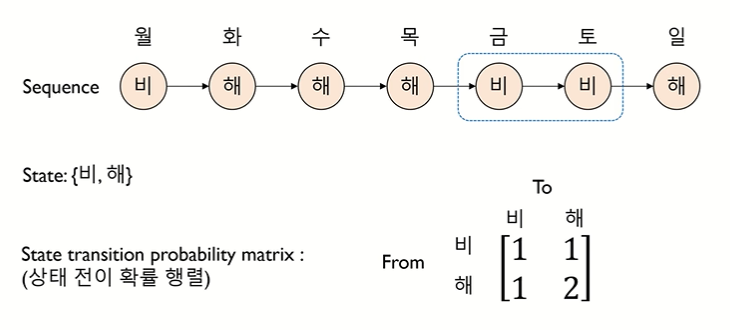
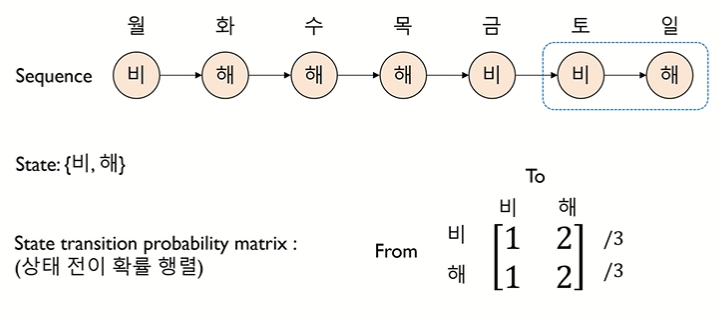
↪ 상태 전이 확률을 sum 으로 나눠주기
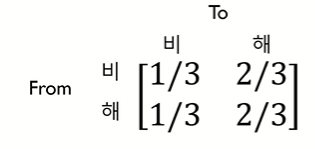
↪ ex. 비에서 비로 갈 확률은 1/3, 비에서 해로 갈 확률은 2/3
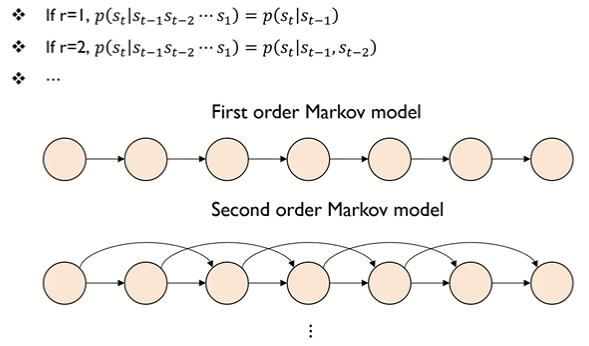
• Markov 가정 : 시간 t 에서 관측은, 가장 최근 r 개의 관측에만 의존한다는 가정. 한 상태에서 다른 상태로의 전이는 이전 상태의 긴 이력을 필요치 않다는 가정
◯ Parameters of the Markov model
• 상태 전이 확률 행렬 A(aij)
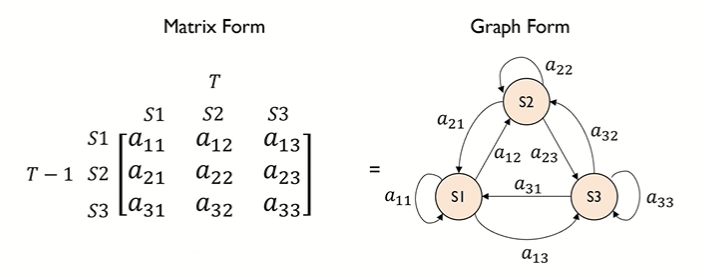
↪ aij 들은 모두 확률값
◯ Hidden Markov model 이란
• 같은 시간에 발생한 두 종류의 state sequence 각각의 특성과 그들의 관계를 이용해 모델링
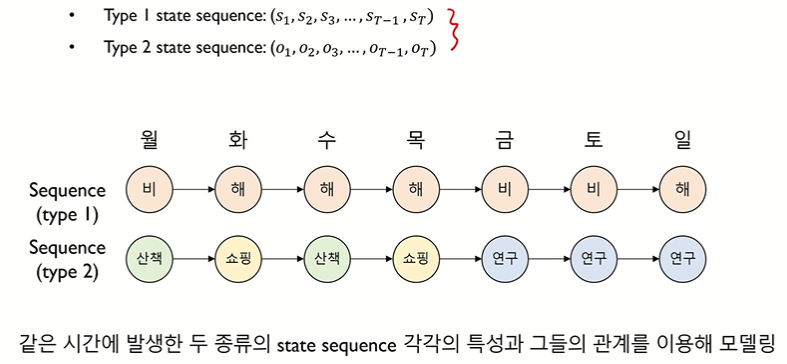
• Hidden 과 Observable
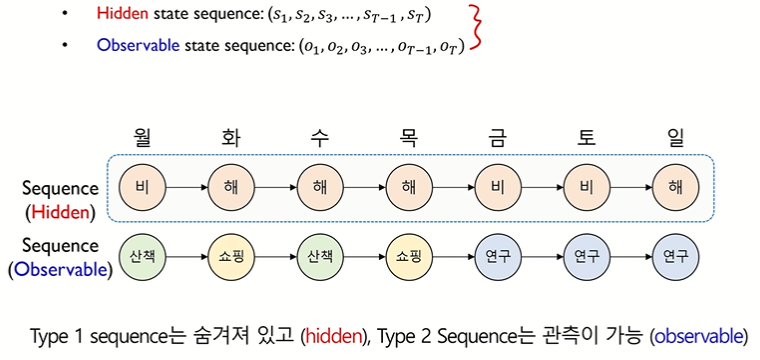

↪ Hidden sequence 인 날씨는 가까운 시점의 과거에만 의존 (Markov 가정을 따름)
↪ ex. 해가 뜬다는 가정 하에 쇼핑을 할거다 : Observable sequence 는 순차적 특성을 반영하는 Hidden sequence 에 종속된다. (조건부 확률의 개념)
• 위의 예제를 그래프 형태로 표현한 것
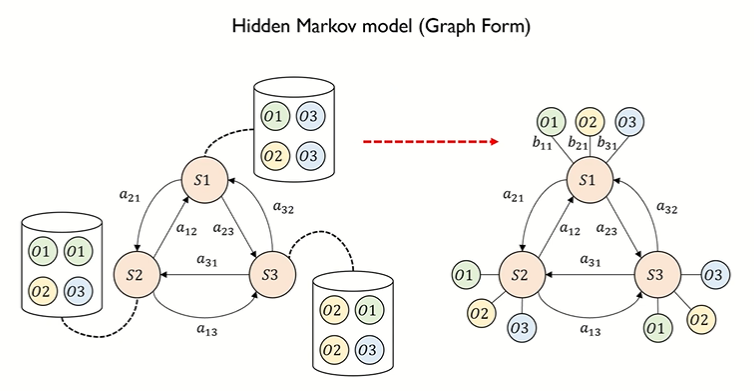
↪ O1,O2,O3 : 관측가능한 상태
↪ S1,S2,S3 : hidden state
↪ aij : hidden state 의 전이확률
• HMM 예제

◯ Parameters
• A(aij) : 상태전이확률 행렬 (hidden state 들이 어떻게 전이 되었는지 from - to 확률을 담아놓은 행렬)
• B(bjk) : Emission probability matrix 방출확률 행렬
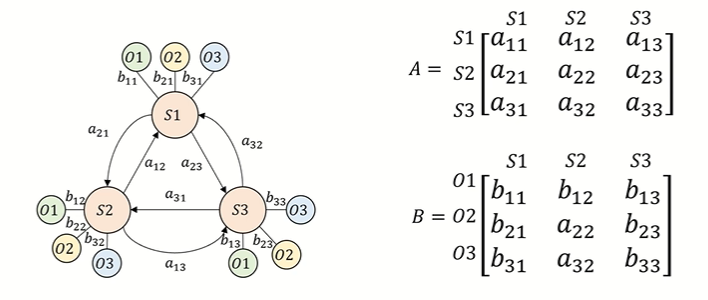
• B 행렬 설명
↪ b11 : S1 상태에서 관측치 O1 을 보게될 확률 , b21 : S1 상태에서 관측치 O2 을 보게될 확률 , b31 : S1 상태에서 관측치 O3 을 보게될 확률
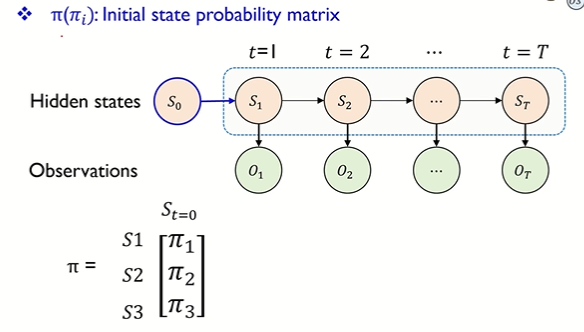
• π(πi) : Initial state probability matrix : 각 hidden state 의 초기 확률
• 3가지 종류의 파라미터 정리
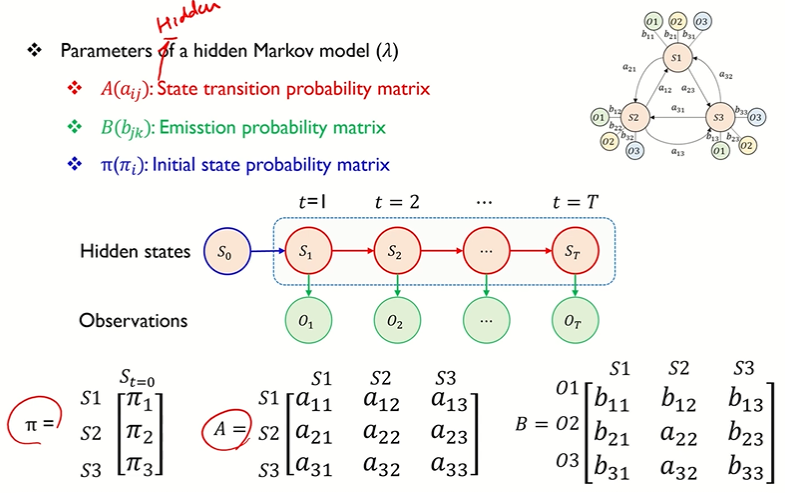

↪ HMM 의 파라미터 : λ = {A,B,π}
↪ aij : t 시점에 i 라는 상태에 있다가, 다음인 t+1 시점에 j 라는 상태로 도달할 확률
↪ bj(vk) : t 시점에 은닉상태 bj 에서 관측치 vk 가 도출될 확률
↪ πi : Si 에서 시작할 확률 (초기값)
◯ Main Problems of HMM
▢ HMM 의 3가지 문제

⑴ HMM(λ*) 파라미터가 추정된 히든 마르코프 모델이 주어지고 O (observable state) 가 주어졌을 때, 그 O (observable state) 의 확률 ⇨ Evaluation problem
⑵ HMM(λ*) 파라미터가 추정된 히든 마르코프 모델이 주어지고 O (observable state) 가 주어졌을 때, 그에 해당하는 hidden state sequence S 를 찾는 것 ⇨ Decoding problem ⭐
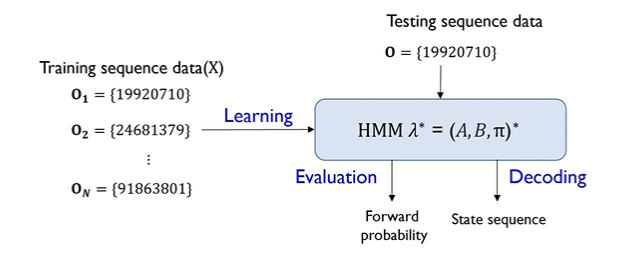
⑶ X={O1, ... , ON} 관측가능한 상태 (=데이터) 들이 주어졌을 때, HMM(λ*) 를 찾는 것 ⇨ Learning problem (1,2 번 과정을 하기 위한 필수적으로 선행되어야 하는 단계 = parameter estimation)
⇨ (3) 의 단계는 모델링이라 보면 되고, HMM 으로 풀 수 있는 궁극적인 문제는 (1), (2) 에 해당
▢ HMM 모델 과정 : 먼저 observable data 로 Learning 을 진행, 이후 Test data 로 만들어놓은 모델을 이용해서 Evaluation 문제 혹은 Decoding 문제를 푼다.
② HMM - Part1 (Evaluation)
◯ HMM - Evaluation
▢ Evaluation 정의
• Evaluation Problem : HMM(λ*) 와 O 가 주어졌을 때, O (observable sequence) 의 확률을 찾기
• Solution : Forward algorithm
• Example : 정박사가 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑할 확률은 ?
↪ probability(O) = (o1 = 산책, o2 = 산책, o3 = 연구, o4 = 쇼핑)
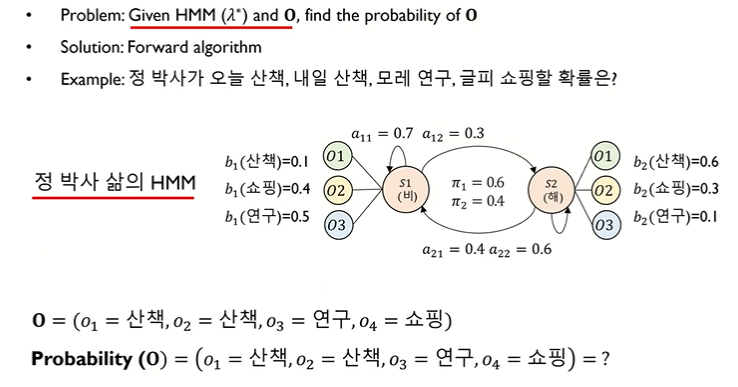
• Graph form : HMM 의 parameter 를 표현하고 있음 (Learning 단계를 통해 얻어낸 결과)
↪ π1, π2 : initial probability (비가 올 확률은 0.6, 해가뜰 확률은 0.4)
↪ a11 : hidden state 의 transition probability (오늘 비오고 내일 또 비가 올 확률 : 0.7)
↪ b1(산책) : 비가 오는 날에 산책을 할 확률이 0.1
▢ Evaluation 문제점
• 그러나 확률을 구하려면 총 16개의 상황을 생각해 보아야 한다 : (hidden state 개수)^(sequence 요소 개수)

↪ 여기서는 state 가 2개고, sequence 가 4개니까 2^4 = 16가지 경우를 고려

↪ 총 상태의 개수나 sequence 길이가 증가하면 계산을 못할 수도 있음 (구해야 될 확률의 가지수가 너무 많으면 문제를 풀 수가 없음) 👉 해결하기 위해 나온 방법이 forward 알고리즘
◯ HMM - Evaluation : Forward algorithm
▢ forward 알고리즘
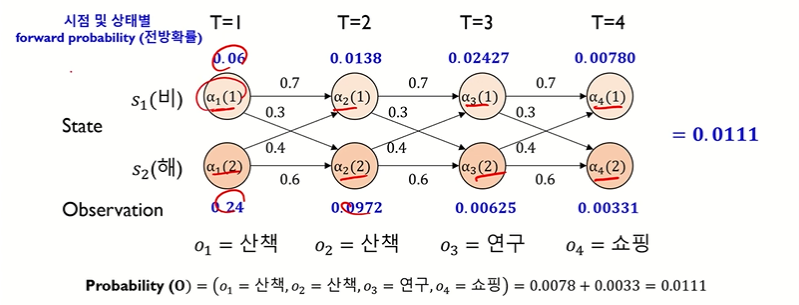
[시점 t = 1]
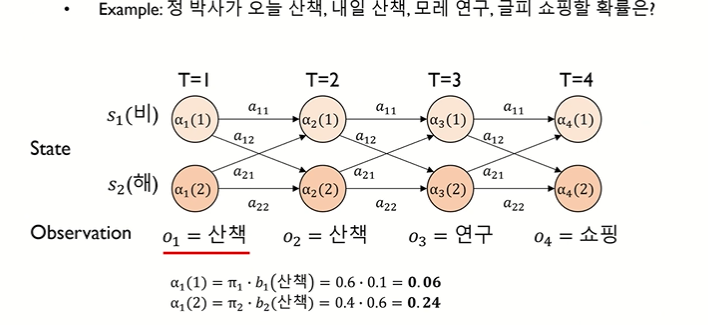
• α1(1) = (첫 번째 시점에서 비올 확률) • (비가 올 hidden 상태에서 산책이 관찰될 확률) = π1•b1(산책)
• α1(2) = (첫 번째 시점에서 해가 뜰 확률) • (해가 뜰 hidden 상태에서 산책이 관찰될 확률) = π2•b2(산책)
[시점 t = 2]
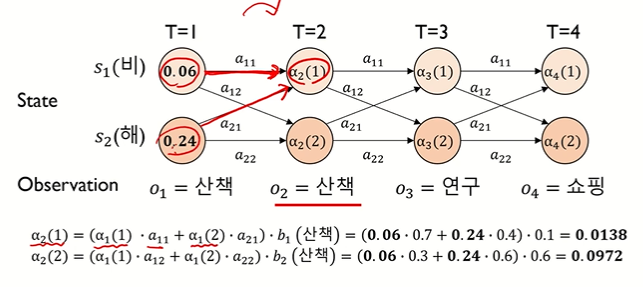
• α2(1) = { α1(1)•a11 + α1(2)•a21 } • b1(산책)
• α2(2) = { α1(1)•a12 + α1(2)•a22 } • b2(산책)
[시점 t = 3]
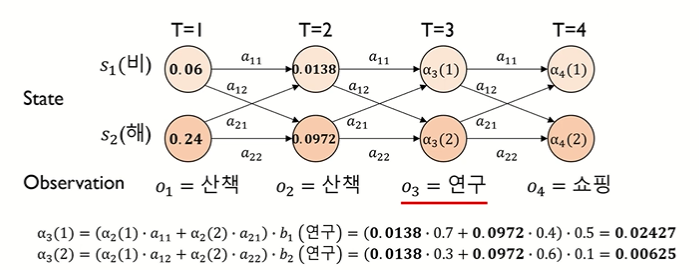
• α3(1) = { α2(1)•a11 + α2(2)•a21 } • b1(연구)
• α3(2) = { α2(1)•a12 + α2(2)•a22 } • b2(연구)
[시점 t = 4]
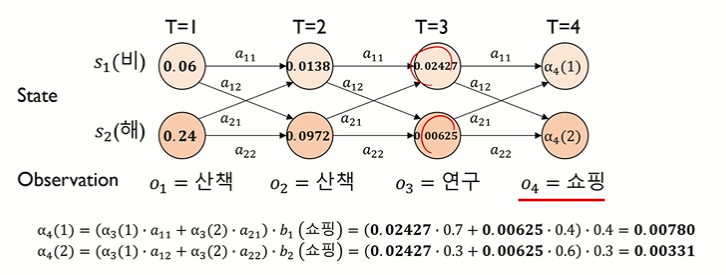
• α4(1) = { α3(1)•a11 + α3(2)•a21 } • b1(쇼핑)
• α4(2) = { α3(1)•a12 + α3(2)•a22 } • b2(쇼핑)
※ 숫자 표기에서, 시점을 나타내는 건지 state 를 나타내는 건지 구분 주의하기!
👉 각 단계에서 활용하는건 바로 직전 시점에 대한 값들로, 빠른 계산이 가능하다. 건너 건너 과거를 보면 과거 정보가 누적되어서 표현된다. 즉, 모든 과거 정보를 가지고 있다 : Forward 알고리즘 (dynamic programming 방법의 핵심)
[최종 확률 계산]
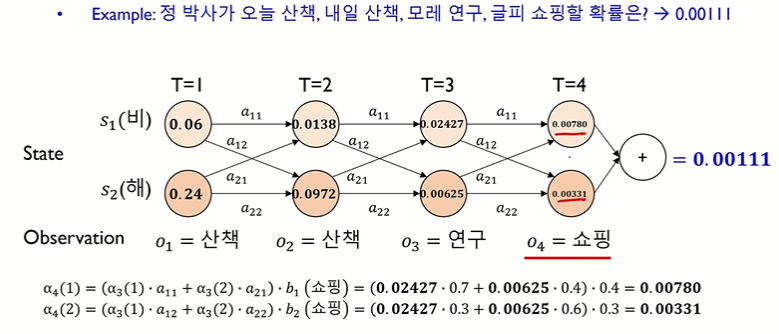
• α4(1) + α4(2) = 0.00111
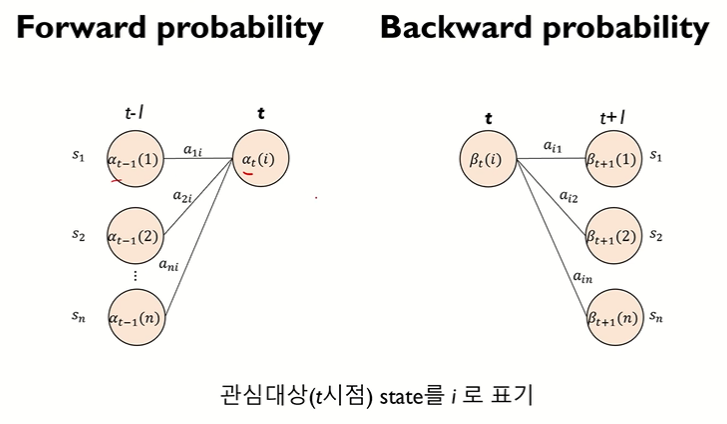
▢ forward probability : α
• 이전 시점의 확률 정보들을 다 안고 계속 앞으로 가는 것이 핵심!
• 이전 시점의 정보만 가지고 빠르게 계산 (그러나 결국에는 과거 정보를 모두 안고 가는 것과 동일)
• 수학 기호 식

• Evaluation problem 은 sequence classification 문제에 활용이 가능하다. 가령 정박사 문제를 해결하는데 있어서 HMM1 모델이 있고, 조박사 문제를 해결하는데 HMM2 모델이 있을 때 (= 두 사람의 패턴이 다름) , 예를 들어 [산책, 산책, 연구, 쇼핑] 이라는 sequence 에서 정박사는 0.78 이 나왔고 조박사는 0.25가 나왔다면 [산책, 산책, 연구, 쇼핑] 이 sequence 는 조박사보다 정박사로부터 나왔을 확률이 높은 것 (여기서 class 는 정박사와 조박사 2개가 되는 것)
• ex. sequence classification : 제조 문제에서는 sequence 가 주어졌을 때 불량에서 나온건지 아닌지
▢ backward probability
◯ HMM - Evaluation : Backward algorithm
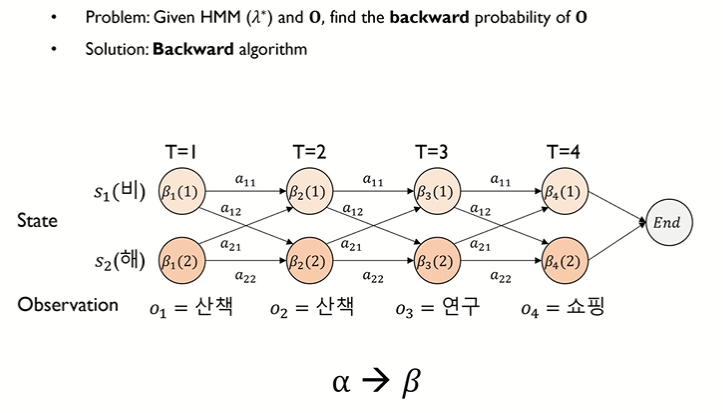
• forward 와 달리 뒤에서부터 계산
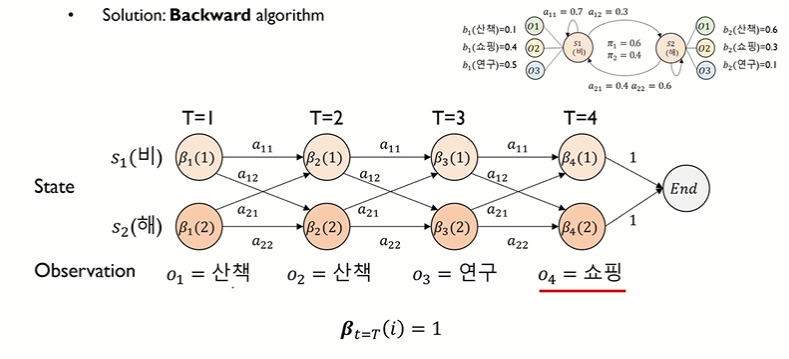
[시점 t = 3]
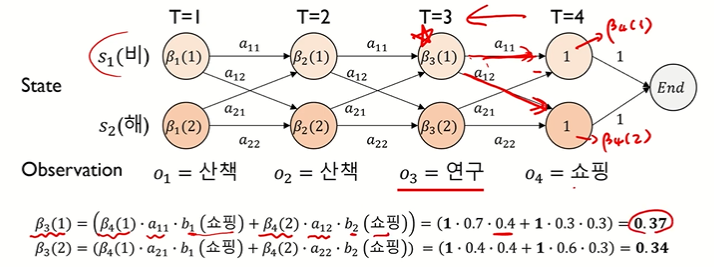
• β3(1) = { β4(1)•a11•b1(쇼핑) + β4(2)•a12•b2(쇼핑) }
• β3(2) = { β4(1)•a21•b1(쇼핑) + β4(2)•a22•b2(쇼핑) }
[시점 t = 2]
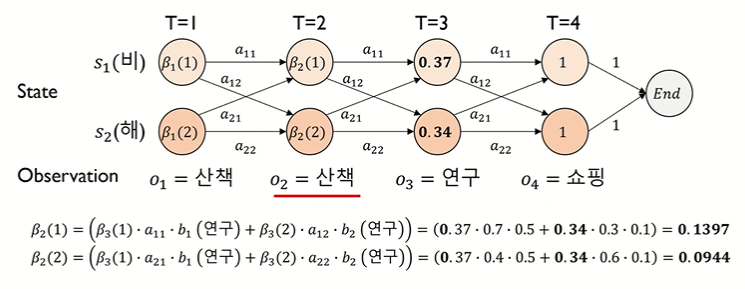
[시점 t = 1]
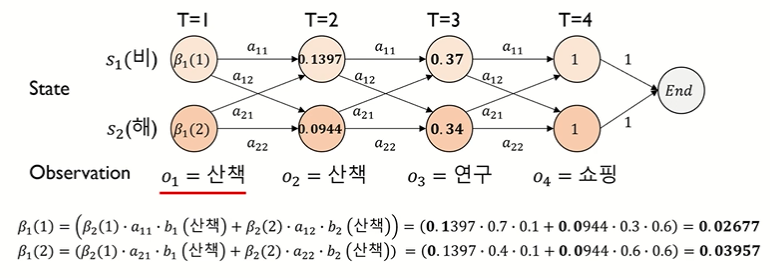
[최종 확률 계산]

▢ backward 와 forward 의 최종 확률 결과는 같아야 한다.

• 수식

• forward/backward probability 👉 HMM training 에 활용 (Learning)
▢ [참고] 마르코프 가정 (독립성 가정) : Observed variable 과 Hidden state 관계 : P(Yt | Ct)
• Yt 가 Ct 에 대해 Conditionally independent 하다는 것은, Yt 가 주어진 현재 상태 Ct 를 알고나면 다른 모든 변수나 상태와는 독립적이라는 것을 의미한다. 즉, 현재 상태 Ct 가 주어진 상태에서 Yt 의 확률분포는 이전의 관찰된 변수나 상태들에 독립적이다.
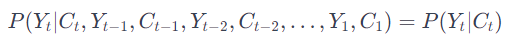
'1️⃣ AI•DS > 📙 Model' 카테고리의 다른 글
| HMM 기본 코드/응용사례 정리 (0) | 2024.01.05 |
|---|---|
| HMM 기초 개념 정리 - ② Decoding, Learning (1) | 2024.01.04 |
| Tabnet (0) | 2022.03.31 |



댓글