📌 필사 노트 링크 : https://colab.research.google.com/drive/1VSgK7OgpsliYQBj7dG2cTb8E_uEistwq?usp=sharing
[kaggle] 회귀_파이썬 머신러닝 완벽가이드.ipynb
Colaboratory notebook
colab.research.google.com
😎 대략의 데이터 가공과 모델 최적화를 수행한 뒤, 다시 이에 기반한 여러가지 기법의 데이터 가공과 파라미터 최적화를 반복적으로 수행하는 것이 바람직한 ML 모델 생성 과정이다! 머신러닝 알고리즘을 적용하기 이전에 완벽하게 데이터의 선처리 작업을 수행하라는 의미가 절대 아니다 ❗
1️⃣ 자전거 수요예측
🔹 dataset
- 2011 년 1월부터 2012년 12월까지 날짜/시간, 기온, 습도, 풍속 등의 정보를 기반으로 1시간 간격 동안의 자전거 대여 횟수 기재
✔ 분석 목적
- 자전거 대여횟수 count 예측
✔ 변수
- 목적 변수 : count
- 설명 변수 : 11개 - 범주형(6) , 수치형(4), 날짜형(1)
- data shape : (10886, 12)
✔ model
- 선형회귀 , 릿지회귀, 라쏘회귀
- 회귀 트리 : XGBRegressor, LGBMRegressor, RandomForestRegressor, GradientBoostingRegressor
- 평가지표 : RMSLE, RMSE, MAE
🔸 keypoint
- pd.to_datetime : 날짜형 타입으로의 변경 👉 year, month, day, hour 칼럼 생성
- np.log1p : 로그 변환 👉 변환된 값은 다시 np.expm1 함수로 원래의 스케일로 복원될 수 있다. RMSLE 를 평가지표로 사용할 땐, 로그변환이 적용된 결과를 사용하는 것에 주의하기!
- 👀 Target 값의 분포가 왜곡된 형태를 이루고 있는지 확인 👉 왜곡된 경우 예측 성능이 저하되는 경우가 발생하기 쉬우므로 로그변환으로 정규분포 형태로 만든다.


- 피처의 회귀계수 시각화 : 계수값이 비정상적으로 큰 경우 👉 데이터 타입이 잘못된 경우 (범주형인데 숫자형 카테고리 값이라 수치형으로 간주됨 → 원핫인코딩 적용 get_dummies), 이상치가 존재하는 경우

💫 분석 과정
(1) LinearRegression basic
| 방법 | 결과 |
|
LinearRegression( )
|
RMSLE : 1.165, RMSE : 140.900, MAE : 105.924 |
👀 타깃값인 대여횟수 분포(왼쪽)를 감안하면 RMSE = 140.9 는 예측 오류로서 비교적 큰값이다. 실제 오류값 상위 5개 (오른쪽) 를 살펴보면 오류가 꽤 크다.


(2) LinearRegression with 타겟변수 정규분포 변환
| 방법 | 결과 |
|
LinearRegression( )
|
RMSLE : 1.017, RMSE : 162.594, MAE : 109.286 |
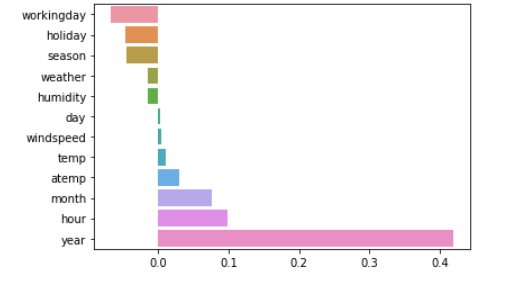
👀 RMSLE 는 줄었지만 RMSE 는 오히려 증가하였다. 회귀계수 값을 시각화 해보니, Year 피처의 회귀계수가 다른 변수에 비해 비정상적으로 큼을 확인해볼 수 있었다. year 는 연도를 뜻하여 값이 (큰) 숫자로 되어있다. 이처럼 숫자형 카테고리 값을 선형회귀에 사용하면 회귀계수 연산에 크게 영향을 받으므로 원-핫 인코딩을 적용해주어야 한다.
(3) 선형회귀 모델들 학습 with 수치형 카테고리 원핫인코딩 적용
X_features_ohe = pd.get_dummies(X_features, columns = ['year', 'month', 'day', 'hour', 'holiday','workingday','season','weather'])
| 방법 | 결과 |
|
LinearRegression( )
|
RMSLE : 0.590, RMSE : 97.688, MAE : 63.382 |
| Ridge(alpha = 10) | RMSLE : 0.590, RMSE : 98.529, MAE : 63.893 |
|
Lasso(alpha =0.01)
|
RMSLE : 0.635, RMSE : 113.219, MAE : 72.803 |
👀 수치형 카테고리 변수들을 원핫인코딩 한 후 모델을 적용해보니 예측 성능이 많이 향상됨
(4) 회귀트리
| 방법 | 결과 |
| RandomForestRegressor(n_estimators=500) | RMSLE : 0.354, RMSE : 50.311, MAE : 31.095 |
|
GradientBoostingRegressor(n_estimators=500)
|
RMSLE : 0.330, RMSE : 53.336, MAE : 32.740 |
|
XGBRegressor(n_estimators=500)
|
RMSLE : 0.345, RMSE : 58.245, MAE : 35.768 |
|
LGBMRegressor(n_estimators=500)
|
RMSLE : 0.319, RMSE : 47.215, MAE : 29.029 |
❗ xgboost 는 데이터프레임 형태가 가닌 ndarray 형태로 입력해야함 : X_train.values
👀 선형회귀모델보다 예측 성능이 많이 개선됨
2️⃣ 주택가격 예측
🔹 dataset
- 미국 아이오와주의 에임스 지방의 주택가격 정보 데이터셋
✔ 분석 목적
- 주택가격에 영향을 미치는 요인 파악, 주택가격 예측
✔ 변수
- 목적 변수 : SalePrice
- 설명 변수 : 80개
- data shape : (1460, 81)
✔ model
- 선형 회귀 모델 : 선형회귀 , 릿지회귀, 라쏘회귀
- 회귀 트리 모델 : XGBRegressor, LGBMRegressor
- 예측결과 혼합을 통한 최종 예측
- 스태킹 앙상블 모델
- 평가지표 : RMSLE, RMSE
🔸 keypoint
✔ RMSLE 평가지표 (https://steadiness-193.tistory.com/277)
- 아웃라이어에 robust 하다. 아웃라이어가 있어도 변동폭이 크지 않다.
- 상대적 error 를 측정해준다. 그러나 금액처럼 크기의 절대값이 민감한 부분의 Error 계산에선 결과 해석이 좋지 않을수도 있다.
- under estimation 에 큰 패널티를 부여한다. 즉 예측값이 실제값보다 작을 때 더 큰 패널티를 부여한다.
✔ baseline modeling 부터 시작하여, 도출된 성능 결과에 계속해서 의문을 던지고, 어떠한 요인들이 그러한 성능을 도출시켰는지 발견하고, 개선방안을 찾아 적용하며 실험해보는 방식 🧐
✔ 선형 회귀, 규제 모델, 회귀 트리, 예측값 혼합, 스태킹 앙상블 등 다양한 접근 및 실험을 시도
✔ 성능 평가 지표 숫자 해석 : 기본적인 모델링을 해보고 추가적인 실험을 통해 값이 낮아지는 것을 확인하는 것이 가장 중요하고, 기본적인 모델링에서 RMSE 값이 너무 큰 경우엔 타겟 데이터의 분포도를 살펴보고 RMSE 값과 비교해보는 작업을 통해 어떤 요인 때문인지 탐색한다.
✔ 회귀 분석에서의 핵심 👉 데이터의 정규성, 회귀 계수 시각화를 통해 예측에 가장 많은 영향을 미치는 중요 변수 찾기, 이상치 데이터 처리
💫 분석 과정 STEP1 - 선형 회귀 모델 학습/예측/평가
(1) Preprocessing
- 데이터 양에 비해 Null 값이 매우 많은 피처 그리고 분석에 불필요한 피처는 drop 한다 : df.drop( [칼럼리스트], axis=1, inplace=True )
- Target 변수의 분포가 정규분포인지 살펴본 후, 치우쳐진 분포라면 로그변환을 통해 정규분포로 만들기 : np.log1p
- Null 값이 많은 수치형 변수에 대해 평균값으로 값 대체 : df.fillna( df.mean( ), inplace=True )
- 문자형 피처 중 카테고리형은 모두 원핫인코딩 변환 : pd.get_dummies( ) 👉 null 값은 None 칼럼으로 대체해주기 때문에 별도의 null 값을 대체하는 로직이 필요 없다. https://devuna.tistory.com/67
(2) 선형회귀 모델 학습
(2)-1. basic
| 방법 | 결과 |
|
LinearRegression( )
|
RMSLE : 0.132 |
|
Ridge( )
|
RMSLE : 0.128 |
|
Lasso( )
|
RMSLE : 0.176 |
👀 라쏘 회귀 방식이 타 회귀방식보다 성능이 떨어지므로 하이퍼 파라미터 튜닝을 시도해볼 필요가 있다.
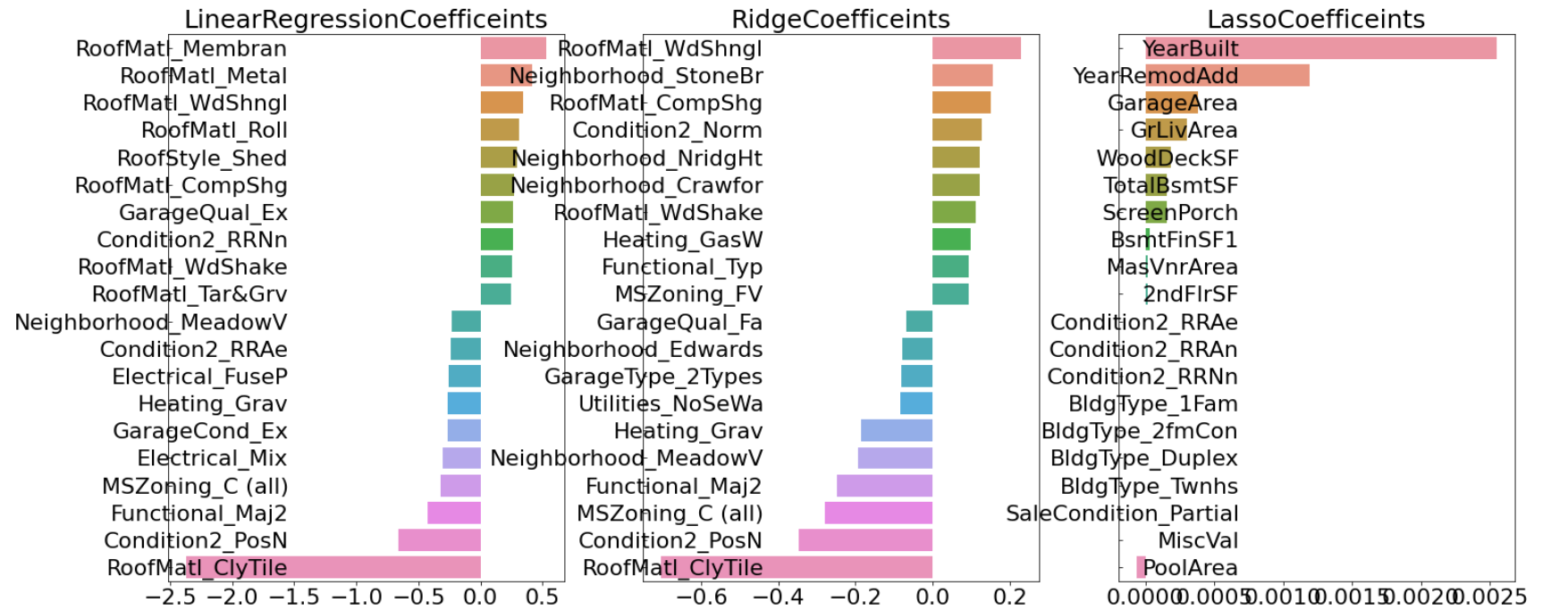
👀 라쏘 회귀 계수의 값은 OLS 기반의 선형회귀와 릿지회귀의 회귀계수 분포 형태와 많이 다르며 값도 매우 작다. 학습 데이터 분할에 문제 때문인지 확인해보기 위해 교차 검증을 수행해본다.
(2)-2. 교차검증 수행
# 데이터를 분할하지 않고 (즉, X_train, y_train 을 사용하지 않고) 전체 데이터로 수행
cross_val_score(model, X_features, y_target, scoring='neg_mean_squared_error', cv=5)
| 방법 | 결과 |
| LinearRegression CV | 평균 RMSLE 값 : 0.155 |
| Ridge CV | 평균 RMSLE 값 : 0.144 |
| Lasso CV | 평균 RMSLE 값 : 0.198 |
👀 라쏘회귀의 성능이 가장 좋은 않은 결과는 동일하므로, 데이터 분할 문제는 아닌 듯 하다.
(3) 릿지와 라쏘 모델의 최적 하이퍼 파라미터 튜닝
- GridSearchCV

- 최적화 alpha 값으로 학습/예측/평가/회귀 계수 시각화
| 방법 | 결과 |
| LinearRegression( ) | RMSLE : 0.132 |
| Ridge(alpha=12) | RMSLE : 0.124 |
| Lasso(alpha=0.001) | RMSLE : 0.12 |
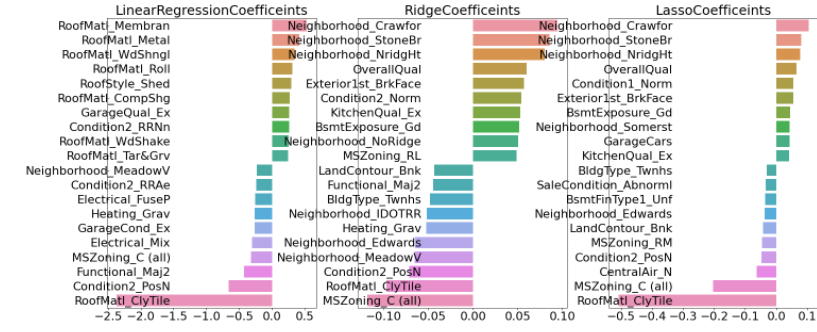
👀 하이퍼 파라미터 튜닝 후 예측 성능이 향상되었고 모델별 회귀계수 값도 많이 달라졌다.
(4) 왜곡이 존재하는 피처 데이터를 정규화 시킨 후 모델링
- 타겟 데이터의 왜곡처럼 지나치게 왜곡된 피처 데이터가 존재할 경우 회귀 예측 성능을 저하시킬 수 있다.
⭐ 왜곡 정도 판단하기 skew( )
- 값이 1 이상인 경우를 왜곡 정도가 높다고 판단한다. 절대적인 기준값은 상황에 따라 편차가 존재한다.
- skew 함수는 숫자형 피처에 적용하는데, 이때 원핫인코딩된 카테고리 숫자형 피처는 제외해야한다.
from scipy.stats import skew
→ 왜곡정도가 높은 피처를 확인하고 (값이 1 이상인 피처) 해당 피처를 로그변환한다.
→ 다시 최적 하이퍼파라미터를 찾아 학습/예측/평가/회귀계수 시각화를 수행한다.
| 방법 | 결과 |
| LinearRegression( ) | RMSLE : 0.128 |
| Ridge(alpha=10) | RMSLE : 0.122 |
| Lasso(alpha=0.001) | RMSLE : 0.119 |
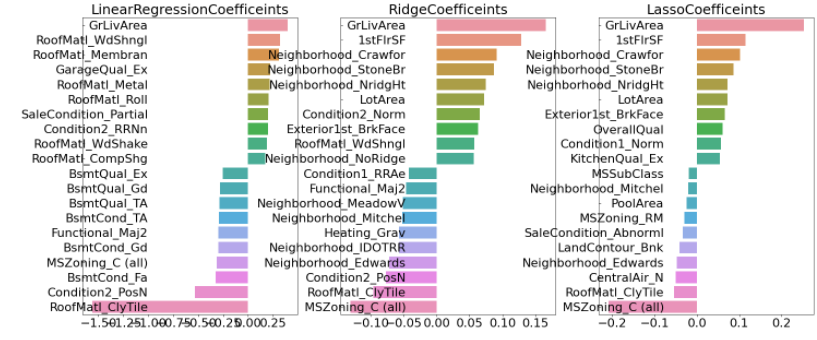
👀 세 모델 모두 GrLiveArea , 즉 주거공간 크기가 회귀계수가 가장 높은 피처가 되었다. 주거공간 크기가 크면 주택 가격에 미치는 영향이 당연히 가장 높을 것이라는 상식선의 결과가 이제야 도출되었다.
(5) 회귀계수가 높은 피처의 이상치 데이터 처리 후 모델링
- 회귀 계수가 높은 피처, 즉 예측에 많은 영향을 미치는 중요 피처의 이상치 데이터의 처리가 중요하다 ⭐
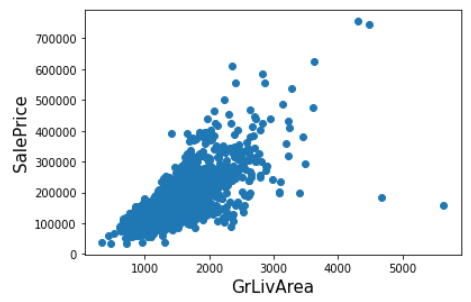

- (4) 의 결과에서 가장 회귀계수 값이 큰 GrLivArea 의 산점도를 시각화했을 때, 오른쪽 끝에 2개의 outlier 관측치를 발견할 수 있었다. 이상치를 제거한 후 다시 릿지와 라쏘 모델 최적화/회귀계수 시각화 를 수행한다.
| 방법 | 결과 |
| LinearRegression( ) | RMSLE : 0.129 |
| Ridge(alpha=8) | RMSLE : 0.103 |
| Lasso(alpha=0.001) | RMSLE : 0.1 |
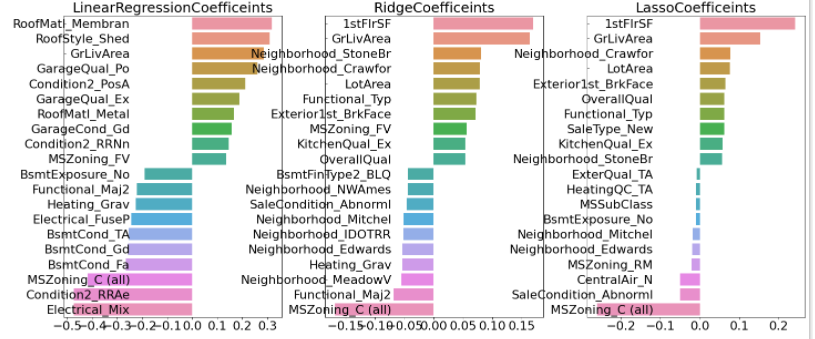
👀 두 개의 이상치만 제거했는데 예측 수치가 매우 크게 향상되었다. GrLivArea 속성이 회귀모델에서 차지하는 영향도가 크기에, 이상치를 개선하는 것이 성능 개선에 큰 의미를 가졌다.
⭐⭐ 이상치를 찾는 것은 쉽지 않으나, 회귀에 중요한 영향을 미치는 피처를 위주로 이상치 데이터를 찾으려는 노력은 중요하다 ⭐⭐
💫 분석 과정 STEP2 - 회귀트리 모델 학습/예측/평가
- 앙상블 부스팅 모델은 시간이 오래걸림
| 방법 | 결과 |
|
XGBRegressor(n_estimators=1000, learning_rate=0.05, colsample_bytree= 0.5, subsample = 0.8)
|
cv RMSLE : 0.115 |
|
LGBMRegressor(n_estimators=1000, learning_rate=0.05, num_leaves=4,
subsample=0.6, colsample_bytree=0.4, reg_lambda=10, n_jobs=-1)
|
cv RMSLE : 0.116 |
- gridsearch 결과에서 feature importance 를 시각화 : model.best_estimator_.feature_importances_
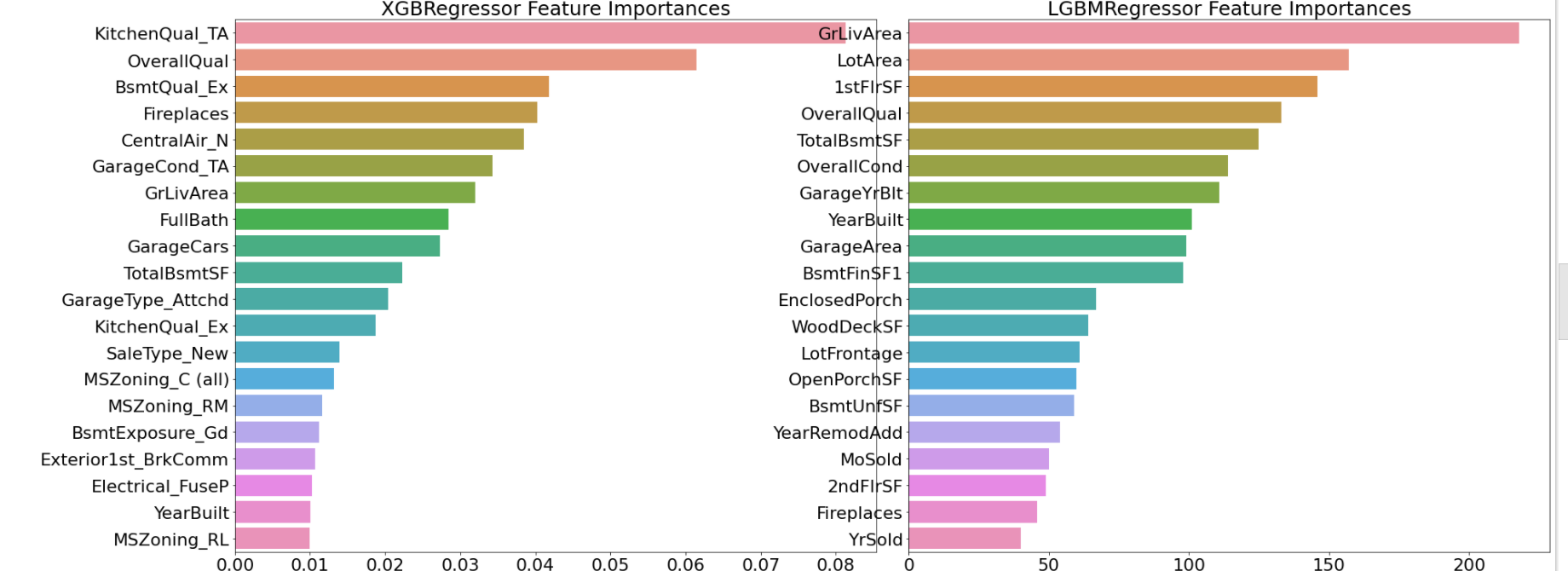
- lgbm 모델의 피처 중요도 결과는 상식선에서 이해가 가는 피처의 분포, xgboost 는 결과 해석이 애매함
💫 분석 과정 STEP3 - 개별 예측 결과 혼합

- 0.4, 0.6 의 특별한 숫자의 기준은 없다. 두 개중 성능이 좀 더 좋은 쪽으로 가중치를 더 두면 된다.
- 릿지와 라쏘 모델의 혼합 결과

- 부스팅 모델의 혼합결과

💫 분석 과정 STEP4 - 스태킹 앙상블
🧐 스태킹 개념 복습
- 두 종류의 모델이 필요 : 개별적인 기반 모델, 최종 메타 모델
- 개별 예측 모델의 예측 데이터를 각각 스태킹 형태로 결합하여 최종 메타 모델의 학습용 피처 데이터 세트와 테스트용 피처 데이터 세트를 만든다.
◻ 검증 데이터 기반 모델 예측 후 데이터 세트 train_fold_pred 👉 최종 메타 모델이 사용하는 학습 데이터
◻ 폴드 세트 내에서 원본 테스트 데이터를 예측한 것의 평균 값 👉 최종 메타 모델이 사용하는 테스트 데이터
# 개별 모델이 반환한 데이터세트를 Stacking 형태로 결합
Stack_final_X_train = np.concatenate((ridge_train, lasso_train,
xgb_train, lgbm_train), axis=1)
Stack_final_X_test = np.concatenate((ridge_test, lasso_test,
xgb_test, lgbm_test), axis=1)
print(Stack_final_X_train.shape)
print(Stack_final_X_test.shape)
# 최종 메타 모델은 라쏘 모델을 적용.
meta_model_lasso = Lasso(alpha=0.0005)
#기반 모델의 예측값을 기반으로 새롭게 만들어진 학습 및 테스트용 데이터로 예측하고 RMSE 측정.
meta_model_lasso.fit(Stack_final_X_train, y_train)
final = meta_model_lasso.predict(Stack_final_X_test)
mse = mean_squared_error(y_test , final)
rmse = np.sqrt(mse)
print('스태킹 회귀 모델의 최종 RMSE 값은:', rmse)
# 스태킹 회귀 모델의 최종 RMSE 값은: 0.0984 로 현재까지 가장 좋은 성능
- 성능 : 0.0984
'3️⃣ Study at Univ > ○ 노트북 필사' 카테고리의 다른 글
| Pycaret - AutoML (0) | 2022.04.13 |
|---|---|
| [kaggle] 2021년 여름방학 필사 스터디 파일 (0) | 2022.04.06 |
| [kaggle] 필사 정리 Note_4 (0) | 2022.03.11 |
| [kaggle] 필사정리 Note_3 (0) | 2022.03.11 |
| [kaggle] 필사정리 Note_2 (0) | 2022.02.18 |

댓글