👀 인과추론 개인 공부용 포스트 글입니다. 출처는 첨부한 링크를 참고해주세요!
① All you need is regression
◯ Review
• 인과추론에서 각 개인에게서 얻을 수 있는 결과 값은 Y0 (처치를 받지 않았을 때 얻는 결과), Y1 (처치를 받았을 때 결과) 이 있다. 그러나 T가 0이나 1로 정해지면 다른 하나의 결과는 영영 알 수 없게 된다. 때문에 개인에 대한 처치효과 δi = Y1i - Y0i 는 알 수 없다.

• 그러나 평균적인 인과 효과 ATE 는 추정할 수 있다 : ATE = E[Y1 - Y0]
• 여기서 일정한 처치효과 k 는 Y1i = Y0i + k 를 만족한다. k 가 양수라면 평균적으로 처치가 양의 효과를 가지고 있다고 말한다.
• 편향 bias 때문에 평균의 차이 E[Y|T=1] - E[Y|T=0] 와 E[Y1-Y0] 는 다르다. 이러한 편향은 처치집단과 비처치 집단이 처치 여부 외에 다른 측면에서 갈라질 때도 발생한다.
• 편향을 확인하는 방법은 두 집단에서 잠재적 결과 Y0 의 차이가 있는지를 보는 것이다.

• 인과추론에서는 이 모든 작업을 한 번에 할 수 있는 도구가 바로 Linear regression 이다. 선형회귀는 조건부 기대함수 CEF 에 대한 최상의 선형 근사치이다.
• 예제

↪ 신경쓰지 않는 모든 것들 (e.g. 시험 당일 학생의 기분, 공부시간 등) 은 ui 항에 포함시킨다.
↪ Online_i : 처치를 받는지를 나타내는 더미변수이다
↪ E[Y|T=0] = δ0 , E[Y|T=1] = δ0 + k ⇨ k 는 ATE
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import graphviz as gr
%matplotlib inline
data = pd.read_csv("data/online_classroom.csv").query("format_blended==0")
result = smf.ols('falsexam ~ format_ol', data=data).fit()
result.summary().tables[1]
• ATE 를 추정할 뿐 아니라 동시에 신뢰구간과 p-value 까지 구할 수 있다.
• ATE = Online 의 모수 추정치에 절편을 더한 값 = 78 + (-4.9) = 73.1
② Regression Theory
◯ Linear prediction



• 하나의 회귀변수 T가 있을 때 그에 대한 파라미터

◯ 회귀변수가 두 개 이상인 경우
• 다른 변수들은 보조적이고 T와 관련된 파라미터 k 를 추정하는데 관심이 있다고 해보자

• T~ : T에 대해 다른 covariates 를 포함한 회귀식 X1i + ... + Xki 의 Residual 잔차 이다.
• 다변량 회귀분석의 계수는 모형의 다른 변수의 효과를 고려한 후 동일한 회귀 분석의 이변량 계수와 같다. 즉, k 는 다른 모든 변수를 사용하여 예측한 후 T의 이변량 계수 (bivariate coefficient) 이다.
※ bivariate coefficient : 두 변수 간의 관계를 나타내는 회귀계수로 두 변수 사이의 상관관계의 강도와 방향성을 설명핸다.
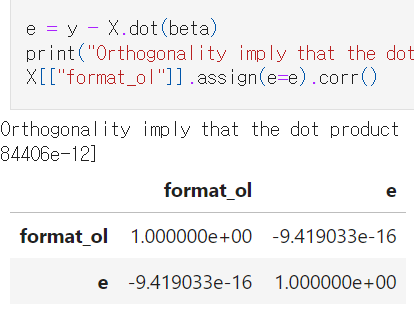
• 다른 변수들로부터 T를 예측할 수 있다면 T는 랜덤이 아니라는 뜻이다. 그러나 다른 변수들을 통제하면 T를 랜덤에 가깝게 만들 수 있다. 선형회귀를 이용해 다른 변수들로부터 T를 예측하고 그 잔차 T~ 를 취한다. 잔차의 정의에 따라 T~ 는 다른 변수 X로부터 예측할 수 없다.
③ Regression for Non-Random Data
◯ Observational data
• 무작위 실험 데이터를 얻기는 어렵다. 따라서 랜덤하지 않은 데이터, 관측 데이터를 다뤄야 한다.
◯ 예제. 추가교육기간이 시간당 임금에 미치는 영향 추정
• 조작변인 T = 교육 받은 기간 , 종속변수 O = 시간당 임금의 로그값
↪ 로그를 사용하면 파라미터 추정치를 백분율로 해석할 수 있게 된다. 즉, 교육기간이 1년 늘어날 때, 임금이 x% 늘어난다고 말할 수 있다. (참고)
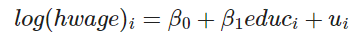
wage = pd.read_csv("./data/wage.csv").dropna()
model_1 = smf.ols('np.log(hwage) ~ educ', data=wage.assign(hwage=wage["wage"]/wage["hours"])).fit()
model_1.summary().tables[1]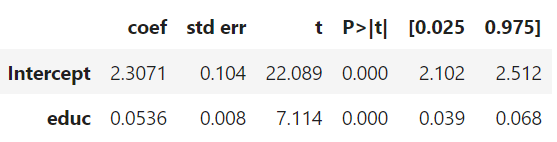
• 모형에 따르면 교육 기간이 1년 추가될 때마다 임금이 약 5.3% 증가한다고 예측할 수 있다. 교육이 임금에 영향을 준다는 가정과 일치하다.
• 그러나 이러한 해석은 믿을만 하지 못하다. 편향이 존재할지도 모르기 때문이다. 따라서 다른 변수들을 통제변수로 활용할 필요성이 있다. meduc, feduc 과 같은 부모의 교육기간, IQ 점수, 경력 연수 exper, 재직 기간 tenure 등이 있다.

• 가령 모형에 IQ 변수를 포함한다면, k 는 IQ 를 고정시키면서 교육기간을 추가했을 때의 반환값이 된다.
• RCT 를 해서 처치집단과 통제집단을 동일하게 만들 수는 없지만, 회귀모형에 다른 요소들을 포함하면 같은 효과를 낼 수 있다.
controls = ['IQ', 'exper', 'tenure', 'age', 'married', 'black',
'south', 'urban', 'sibs', 'brthord', 'meduc', 'feduc']
X = wage[controls].assign(intercep=1)
t = wage["educ"]
y = wage["lhwage"]
beta_aux = regress(t, X)
t_tilde = t - X.dot(beta_aux)
kappa = t_tilde.cov(y) / t_tilde.var()
kappa
• 위의 추정 결과는 0.04가 되는데 이 계수 값은 동일한 IQ, 경력, 재직 기간, 나이 등을 가진 사람들의 경우 교육 기간이 1년 늘어날 때마다 시간당 임금이 4.11% 상승한다는 뜻이다. 이전의 추정값에 비하면 값이 다소 감소했는데, 이렇게 다른 요소들을 통제하고 나면 추정의 영향력은 자연스럽게 감소하게 된다.
④ Omitted variable or Confounding Bias
• 모형에서 모든 교란 변수를 고려한 경우 OVB 가 없다고 말한다.
• 교란변수는 처치와 결과를 모두 유발하는 변수이다.
• IQ-교육-임금 : Postivie bias 예시
• 경찰력-폭력사건-범죄율 : Nevative bias 예시
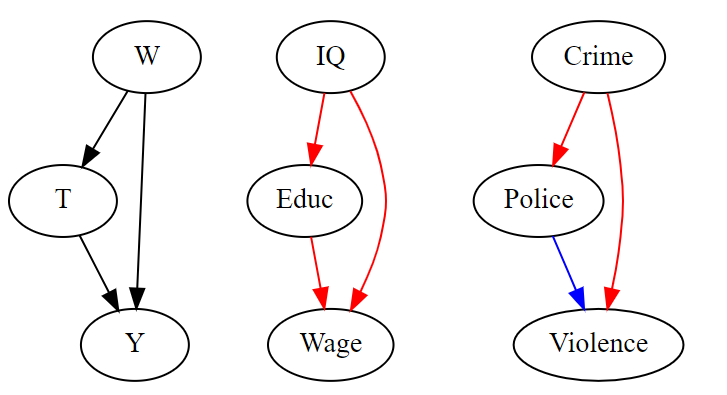
• 회귀분석은 교란변수 W를 고정하고 T의 효과를 비교하여 교란변수의 효과를 보정한다. W가 여전히 T와 Y를 유발하고 있으나, 그 값이 고정되어 있기 때문에 T와 Y의 변화에 영향을 줄 수 없을 뿐이다.
'1️⃣ AI•DS > 🥎 Casual inference' 카테고리의 다른 글
| [The Brave and True] 7. Beyond Confounders (1) | 2023.06.29 |
|---|---|
| [The Brave and True] 6. Grouped and Dummy Regression (0) | 2023.06.28 |
| 인과추론의 데이터 과학 - 인과추론을 위한 머신러닝 모델 (0) | 2023.06.26 |
| [The Brave and True] 4. Graphical causal model (0) | 2023.06.26 |
| [The Brave and True] 3. The-Most-Dangerous-Equation (0) | 2023.06.22 |




댓글