1️⃣ 9강 복습
🔹 Main Topic : GNN 의 표현능력과 범위
• Expressive power : 어떻게 서로다른 그래프 구조를 구별하는가 (node 와 graph structure 를 어떻게 구분하는가)
• Maximally expressive GNN model : 표현력을 어디서 극대화 시킬 수 있을까
🔹 GNN model
① GCN : mean pool
② GraphSAGE : max pool
• Local Neighborhood Structure : 모든 노드가 같은 feature 를 가지고 있는 그래프에서 서로다른 노드를 구별하는 방법 (same color - same feature 로 간주)
↪ 기준1 : different node degree

↪ 기준2 : different neighbors' node degrees

✔ 노드1 과 노드2 는 구조가 완전히 동일 symmetric → same embedding → GNN 은 노드1과 2를 구분해내지 못함

🔹 Computational Graph
• computational graph 는 노도의 Rooted Subtree Structure 에 따라 결정된다.

• 표현력이 좋은 GNN 은 subtree 를 임베딩으로 일대일 대응 Injective 시킨다.

↪ Aggregation 이 이웃노드 정보를 충분히 반영한다면, 노드 임베딩은 서로다른 subtree 를 잘 구분해낼 수 있다.
↪ GNN 의 표현능력은 어떤 이웃노드 aggregation 함수를 쓰느냐에 달려있으며, 일대일함수 성질을 가진 것이 표현력이 가장 좋다고 볼 수 있다.
🔹 Most powerful GNN
• GCN → Not injective
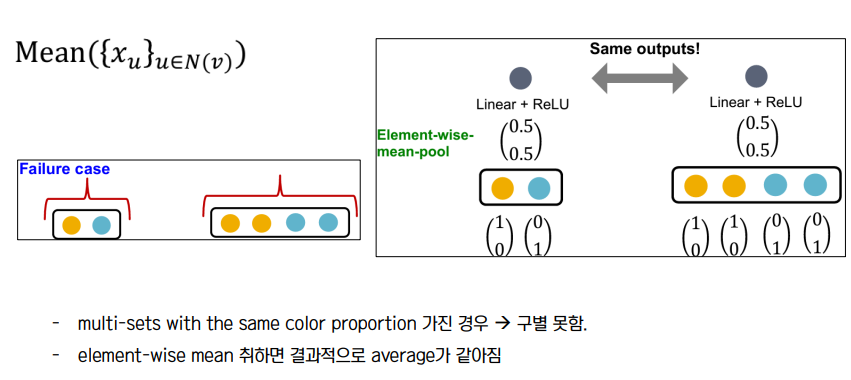
• GraphSAGE → Not injective
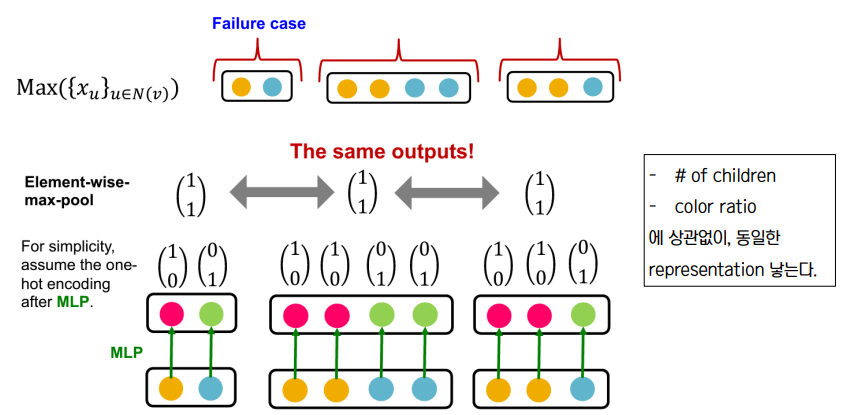
• Graph Isomorphism Network GIN 👉 Most Expressive
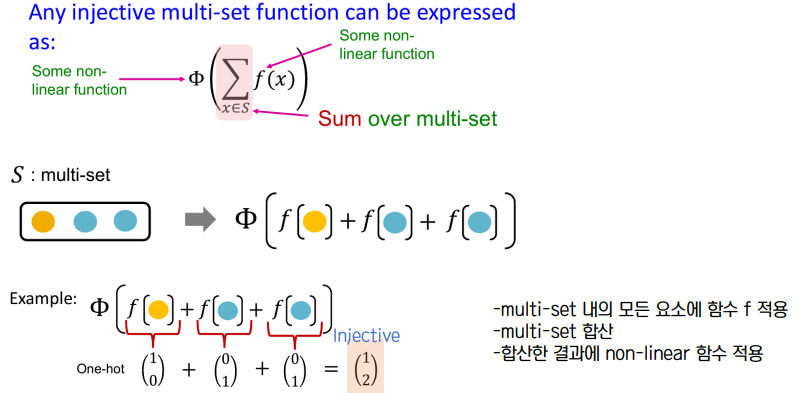

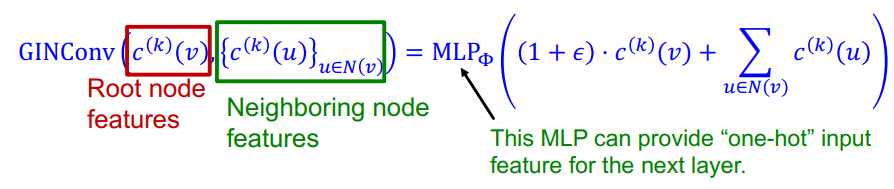
↪ GIN 은 MLP - sum - MLP 구조로 일대일 대응을 가능케 한다.
2️⃣ GIN 리뷰
https://towardsdatascience.com/how-to-design-the-most-powerful-graph-neural-network-3d18b07a6e66
GIN: How to Design the Most Powerful Graph Neural Network
Graph classification with Graph Isomorphism Networks
towardsdatascience.com
🔹 Topic
• graph embedding 을 가능하게 하기 위해, GNN 으로부터 얻은 node embedding 을 어떻게 결합할까 → Global Pooling and GIN
🔹 PROTEINS Dataset
• PROTEINS 데이터셋은 단백질을 표현하는 1113 개의 그래프를 포함하고 있다. 아미노산이 노드에 해당하며 , 두 노드가 0.6 나노미터 미만의 가까운 거리에 있으면 엣지로 연결되어 있다.
• 이 데이터셋을 통해 우리는 각 단백질을 효소인지 아닌지로 구별해내는 과제를 수행한다.

• GraphSAGE 등의 GNN 의 일반적인 모델로 임베딩한 결과가 좋지 않다면, mini-batch 를 통해서 성능을 높일 수 있다. PROTEINS 데이터셋은 크지 않기 때문에 미니배치를 통해 훈련 속도를 높일 수 있다.
train_loader = DataLoader(train_dataset, batch_size= 64, shuffle = True)
val_loader = DataLoader(val_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
🔹 Graph Isomorphism Network
• GIN 은 GNN 의 표현성을 극대화 하기 위해 고안된 모델이다.
① Weisfeiler-Lehman test
GNN 의 표현능력을 정의하기 위해 사용되는 방법에는 WL graph isomorphism test 가 있다.
Isomorphic graph 란 똑같은 구조를 가진 그래프를 의미한다.
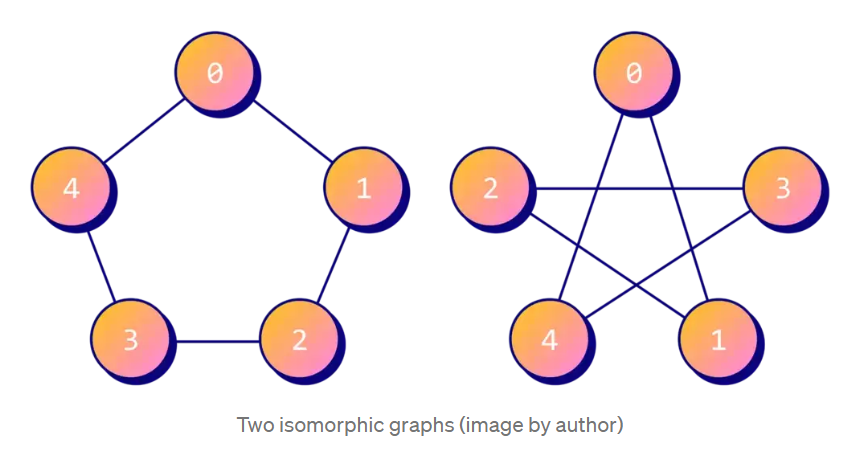
위의 그림과 같이, 똑같은 연결구조를 지녔지만 노드의 위치순서만 바뀐 두 그래프의 관계를 Isomorphic 한다고 말한다. WL test 는 만약 두 그래프가 non-isomorphic 하다면 non-isomorphic 하다고 말해줄 수 있다. 그러나 isomorphic 하다는 것은 말해주지 않는다. 오직 non-isomorphic 의 가능하다 여부만 알려줄 수 있다.
WL test 는 GNN 이 학습하는 방법과 매우 유사하다. WL test 에서는
1. 모든 노드가 동일한 label 을 가지고 시작하며
2. 이웃 노드로부터 얻은 label 정보를 병합하고 해시함수를 적용해 새로운 label 을 형성하는 단계를
3. label 이 더 이상 바뀌지 않을 때까지 반복한다.
의 과정을 통해 학습을 진행하는데, 이는 GNN 에서 feature vector 를 aggregate 하는 방법과 매우 유사할 뿐만 아니라, 그래프 유사성을 판단할 수 있는 능력은 GCN 이나 GraphSAGE 같은 다른 모델들 보다 더 강력한 구조를 갖는다고 볼 수 있다.
② One aggregator to rule them all
WL test 의 장점에 고안하여, 새로운 aggregator 함수를 만들게 되는데, 이 함수는 만약 non-isomorphic 한 그래프들 이라면 서로 다른 노드 임베딩을 생산할 수 있도록 한다. (서로 다른 그래프에 대해 서로 다른 노드 임베딩을 출력)
논문 연구에서는 2개의 일대일 대응 함수를 제안한다.
1. GAT 네트워크를 통해, 주어진 task 에 대해 best weighting factor (최적의 가중치 인자) 를 학습할 수 있도록 한다.
2. GIN 네트워크를 통해, 두 일대일 함수의 근접성을 학습한다. (by Universal Approximation Thm)
↪ Universal Approximation Thm : 충분히 큰 Hidden Dimension 과 Non-Linear 함수가 있다면 1-Hidden-Layer NeuralNet 으로 어떤 연속함수든 근사할 수 있다.
GIN 에서 특정한 노드 i 의 hidden vector (hi) 를 계산하는 수식은 다음과 같다.
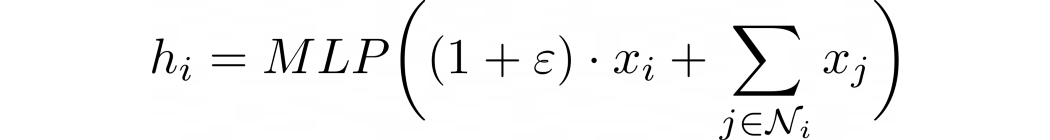
해당 수식에서 ɛ 는 이웃노드와 비교했을 때, target 노드의 중요성을 결정하는 인자로, 만약 이웃노드와 동일한 중요도를 가진다 하면 값이 0이 된다. ɛ 는 고정된 상수값이거나 학습 가능한 파라미터일 수 있다.
③ Global Pooling
그래프 수준의 해석 혹은 Global pooling 은, GNN 을 통해 계산된 노드 임베딩을 가지고 graph embedding 을 만들 수 있다. graph embedding 을 얻는 가장 간단한 방법은 mean, sum, max 연산을 모든 노드 임베딩 hi 에 대해 수행하는 것이다.
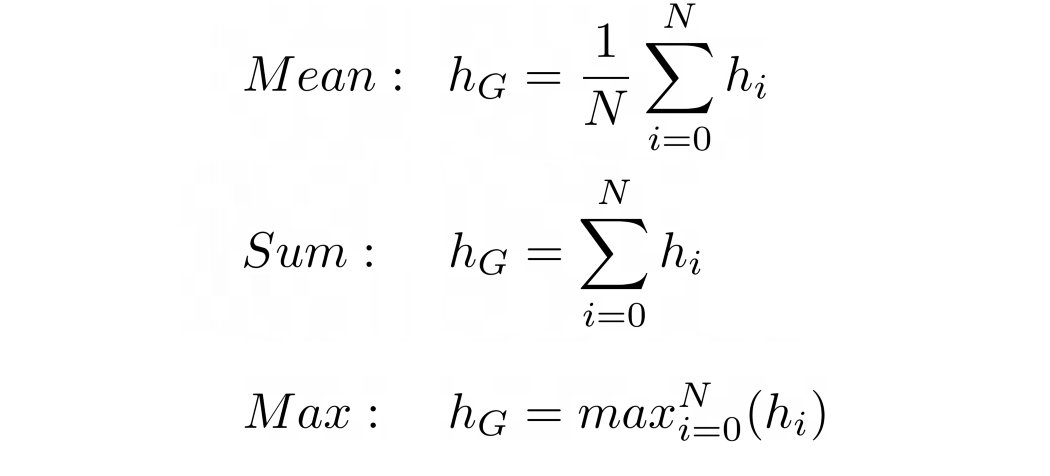
논문 저자는 graph 수준의 해석에 대해 2가지 중요한 사실을 강조한다.
1. 모든 구조적인 정보를 고려하려면, 이전 레이어의 임베딩을 유지 (keep) 하는 것이 필수적이다.
2. mean 이나 max 연산보다 sum 연산자가 가장 표현력이 좋다.
이러한 사실들을 바탕으로 다음과 같은 Global pooling 함수를 제안하게 된다.
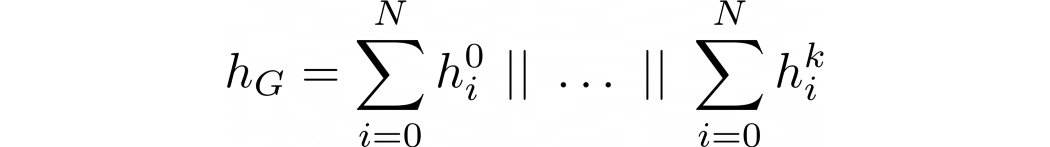
각 레이어에 대해서 노드 임베딩 값은 모두 더해지고, 더한 결과를 모두 concat 시킨다.
🔹 GIN in pytorch
• GINConv
↪ nn : MLP (두 일대일 대응 함수를 근접시키는데 사용)
↪ eps : ɛ 의 초기값 (보통 0으로 설정)
↪ train_eps : ɛ 가 훈련 가능한 파라미터인지 T/F 로 표기 (보통 F 로 설정)
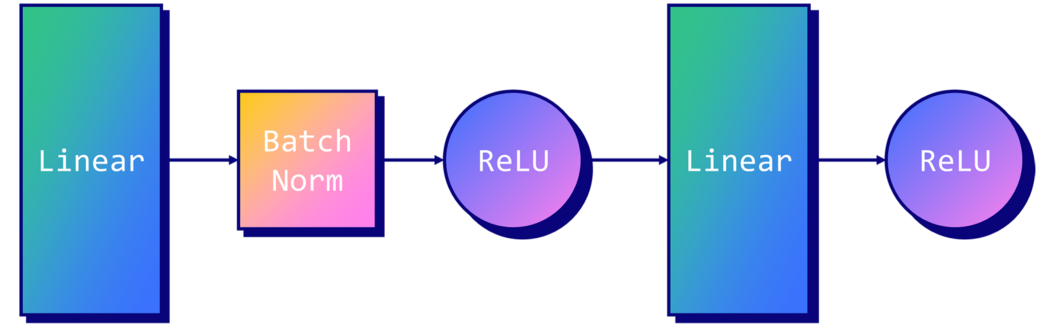
[참고] GINEConv
↪ Second GIN layer , 이웃노드의 feature 에 ReLU function 을 적용시킨다.
3️⃣ 코드리뷰
https://colab.research.google.com/drive/1ycQVANLkgqyk_iezLYGbSUp98JsY7bEQ?usp=sharing
9강 복습과제.ipynb
Colaboratory notebook
colab.research.google.com
• GCN 과 성능을 비교해볼 예정
🔹 GIN architecture code
• Library
from torch.nn import Linear, Sequential, BatchNorm1d, ReLU, Dropout
import torch.nn.functional as F
from torch_geometric.nn import GCNConv, GINConv #✨
from torch_geometric.nn import global_mean_pool, global_add_pool #✨
• GCN
class GCN(torch.nn.Module) :
def __init__(self, dim_h) :
super(GCN, self).__init__()
self.conv1 = GCNConv(dataset.num_node_features, dim_h)
self.conv2 = GCNConv(dim_h, dim_h)
self.conv3 = GCNConv(dim_h, dim_h)
self.lin = Linear(dim_h, dataset.num_classes)
def forward(self, x, edge_index, batch) :
# 노드 임베딩
h = self.conv1(x, edge_index)
h = h.relu()
h = self.conv2(h, edge_index)
h = h.relu()
h = self.conv3(h, edge_index)
# 그래프 level 해석 (graph embedding)
hG = global_mean_pool(h, batch)
# 분류기
h = F.dropout(hG, p=0.5, training = self.training)
h = self.lin(h)
return hG, F.log_softmax(h, dim=1) # 효소인지 아닌지 분류
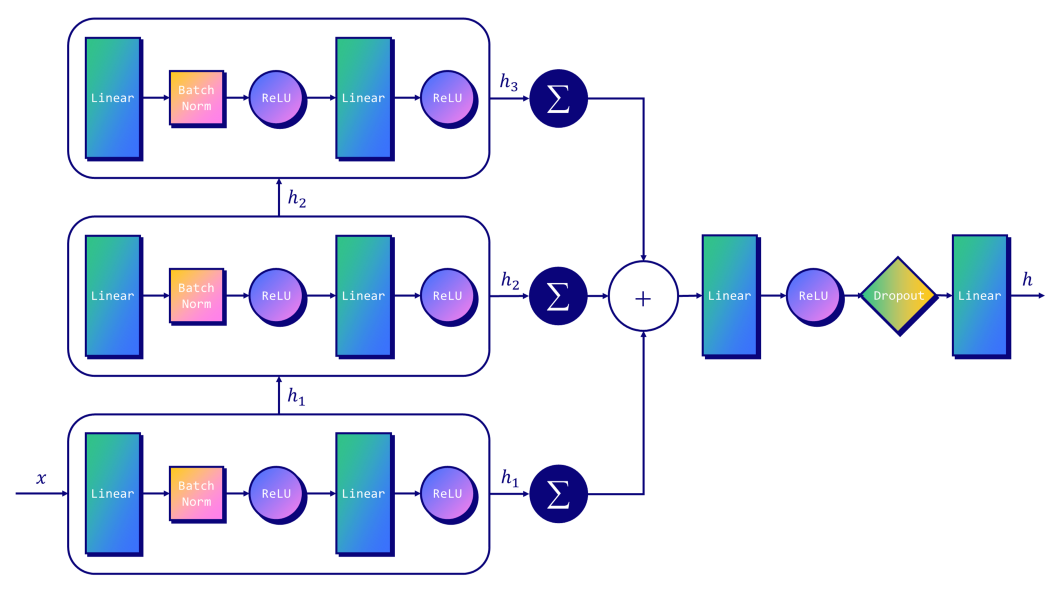
• GIN (3 layer)
class GIN(torch.nn.Module) :
def __init__(self, dim_h) :
super(GIN, self).__init__()
self.conv1 = GINConv(
Sequential(Linear(dataset.num_node_features, dim_h),
BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU())
)
self.conv2 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU())
)
self.conv3 = GINConv(
Sequential(Linear(dim_h, dim_h), BatchNorm1d(dim_h), ReLU(),
Linear(dim_h, dim_h), ReLU())
)
self.lin1 = Linear(dim_h*3, dim_h*3)
self.lin2 = Linear(dim_h*3, dataset.num_classes)
def forward(self, x, edge_index, batch) :
# 노드임베딩
h1 = self.conv1(x, edge_index)
h2 = self.conv2(h1, edge_index)
h3 = self.conv3(h2, edge_index)
# 그래프 level 해석 (graph embedding)
h1 = global_add_pool(h1, batch)
h2 = global_add_pool(h2, batch)
h3 = global_add_pool(h3, batch)
# concate 그래프 임베딩
h = torch.cat((h1,h2,h3), dim = 1)
# 분류기
h = self.lin1(h)
h = h.relu()
h = F.dropout(h, p = 0.5, training = self.training)
h = self.lin2(h)
return h, F.log_softmax(h, dim=1)
gcn = GCN(dim_h=32)
gin = GIN(dim_h=32)
• Train and Test
def train(model, loader) :
criterion = torch.nn.CrossEntropyLoss() # 💡 평가지표
optimizer = torch.optim.Adam(model.parameters() , lr = 0.01, weight_decay = 0.01) # 💡 최적화
epochs = 100
model.train()
for epoch in range(epochs +1) :
total_loss = 0
acc = 0
val_loss = 0
val_acc = 0
# 💡 배치 단위로 학습
for data in loader :
optimizer.zero_grad()
_, out = model(data.x, data.edge_index, data.batch)
loss = criterion(out, data.y)
total_loss += loss / len(loader)
acc += accuracy(out.argmax(dim=1), data.y) / len(loader)
loss.backward()
optimizer.step()
# 💡 validation
val_loss, val_acc = test(model, val_loader)
# 10 epoch 마다 지표값 출력
if (epoch%10 == 0) :
print(f'Epoch {epoch:>3} | Train Loss: {total_loss:.2f} '
f'| Train Acc: {acc*100:>5.2f}% '
f'| Val Loss: {val_loss:.2f} '
f'| Val Acc: {val_acc*100:.2f}%')
test_loss, test_acc = test(model, test_loader)
print(f'Test Loss: {test_loss:.2f} | Test Acc: {test_acc*100:.2f}%')
return model
def test(model, loader):
criterion = torch.nn.CrossEntropyLoss()
model.eval()
loss = 0
acc = 0
for data in loader:
_, out = model(data.x, data.edge_index, data.batch)
loss += criterion(out, data.y) / len(loader)
acc += accuracy(out.argmax(dim=1), data.y) / len(loader)
return loss, acc
def accuracy(pred_y, y):
"""Calculate accuracy."""
return ((pred_y == y).sum() / len(y)).item()
🔹 test accuracy result

• 성능차이가 발생하는 이유
↪ GCN 과 달리, GIN 의 aggregator 는 특히 graph 를 판별하는데 고안된 모델구조이다.
↪ GIN 은 맨 마지막 hidden vector 만을 고려하는 것이 아니라, 모든 레이어의 hidden vector 를 concat 함으로써 그래프 전체 구조를 고려한다.
↪ sum 연산이 mean 연산보다 더 성능이 뛰어나다 (injective 면에서)
• Graph classification 결과

• GCN 결과와 GIN 결과를 ensemble 하여 성능을 조금 더 높일 수 있다. normalized 된 output vector 에 평균을 취하는 방식으로 두 네트워크의 그래프 임베딩 결과를 결합한다.
gcn.eval()
gin.eval()
acc_gcn = 0
acc_gin = 0
acc = 0
for data in test_loader :
# 분류
_, out_gcn = gcn(data.x, data.edge_index, data.batch)
_, out_gin = gin(data.x, data.edge_index, data.batch)
out = (out_gcn+ out_gin)/2 # ✨
# accuracy score 계산
acc_gcn += accuracy(out_gcn.argmax(dim=1), data.y) / len(test_loader)
acc_gin += accuracy(out_gin.argmax(dim=1), data.y) / len(test_loader)
acc += accuracy(out.argmax(dim=1), data.y) / len(test_loader)

🔹 Conclusion
GIN 은 GNN 을 이해하는 데 있어서 매우 중요한 네트워크이다. 정확도를 향상시킬 뿐만 아니라, 여러가지 GNN 구조 중에서 어떠한 모델이 가장 표현력이 좋은지 이론적으로 설명가능할 수 있도록 만든 네트워크라 볼 수 있다.
해당 아티클에서는 graph classification task 에 대해 global pooling 을 수행하기 위하여, WL test 아이디어에서 고안된 GIN 네트워크를 적용해보는 내용을 담고 있다.
비록 PROTEINS 데이터에 대해서는 GIN 이 좋은 성능을 보였으나, social graph 와 같이 실제 세계 데이터에는 잘 적용되지 않는 경우도 있다.
'1️⃣ AI•DS > 📘 GNN' 카테고리의 다른 글
| [cs224w] Frequent Subgraph Mining with GNNs (0) | 2023.01.27 |
|---|---|
| [CS224W] Graph Neural Network (0) | 2022.11.24 |
| [CS224W] Message Passing and Node classification (0) | 2022.11.17 |
| [CS224W] PageRank (0) | 2022.11.02 |
| [CS224W] 1강 Machine Learning With Graphs (0) | 2022.10.11 |




댓글