논문
1️⃣ Abstract
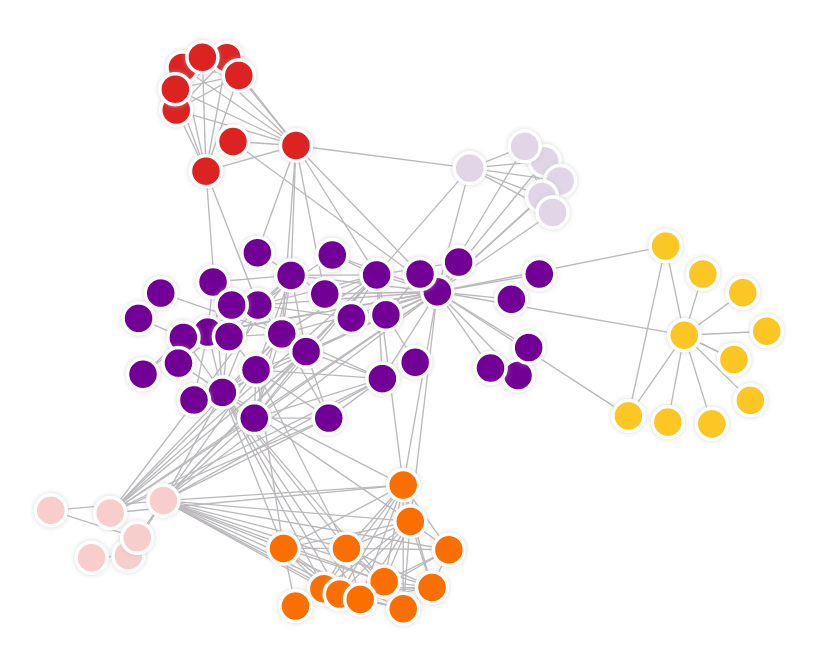
① 문제점 제시
• graph clustering 에서 "비지도학습" 에 관한 발전이 더디게 이루어지고 있다.
• graph clustering 기법이 낮은 성능을 보인다.
② 해결 방안
• DMoN : Deep Modularity Networks : 비지도 풀링 학습 방법
▸ graph pooling : https://greeksharifa.github.io/machine_learning/2021/09/09/GraphPooling/
Python, Machine & Deep Learning
Python, Machine Learning & Deep Learning
greeksharifa.github.io
↪ 노드 임베딩들로부터 그래프 임베딩을 얻는 과정을 의미한다. 간단하게 말하자면, full graph, 즉 전체 그래프에서 크기와 밀도를 줄여 subgraph 를 생성하는 과정으로 생각해볼 수 있다. 이때 subgraph 는 일반적으로 전체 그래프에서 일부분을 뜻함과 헷갈리지 않아야 한다.
▸ Modularity Clustering : 그래프를 계층적으로 클러스터링하는 방법으로, 클래스터 내부의 링크와 그 링크들간의 밀집도를 기반으로 modularity 를 계산해 가장 높은 modularity 를 갖는 클러스터들로 구성하기 위해 사용되는 방법
↪ modularity : measures the strength of division of a network into modules (also called groups, clusters or communities). Networks with high modularity have dense connections between the nodes within modules but sparse connections between nodes in different modules.
2️⃣ Introduction
① Cluster in Graph
• 그래프는 cluster (= communities = modules) 들을 형성하며 지역적으로 비동질적(inhomogeneous) edge 분포를 보인다.
• cluster 는 높은 edge (link) 밀집도를 보이는 노드들의 집합을 의미한다.
• cluster 를 정의함으로써 교육이나 고용 분야와 같은 social graph 에서 흥미로운 현상들을 발견해낼 수 있다.
② Problem of Recent works about GNNs (in Clustering)
• 고차원 구조를 활용하는 GNN 의 대부분에 관한 연구는 node partitioning 이나 clustering 에 직접적으로 관여하는 경우가 드물다. 특히 비지도학습의 그래프 클러스터링 방법을 제외하고 semi-supservised 혹은 supervised 프레임워크만을 다루는 사례가 많다.
※ semi-supervised learning : 소량의 labeled data에는 supervised learning을 적용하고 대용량 unlabeled data에는 unsupervised learning을 적용해 추가적인 성능향상을 목표로 하는 방법론. unlabeled data 를 사용하기 때문에 generalization 에 유리하다.
• 현존하는 비지도학습 알고리즘 대부분은 multi-step optimization 방식에 의존하고 있으며, 종단의 미분가능한 목적함수 (end-to-end differentiable objective) 를 사용하지 않는다는 문제점이 있다.
③ Solution
• Conntection between Graph Pooling ( supervised GNN ) and fully unsupervised Clustering 👉 DMoN
↪ GNN 을 활용한 비지도학습 클러스터링 모듈인 DMoN 은 클러스터링 과제에서 종단의 미분가능한 방식으로 최적화 방식을 사용할 수 있도록 한다.
3️⃣ Related Works
① GNNs
• allow end-to-end differentable losses over data with arbiturary structure
• applications : social networks, recommender systems, computational chemistry
• GNN 은 비지도학습의 손실함수를 사용해도 될 만큼 유연한 네트워크에 해당하지만, node classification 등의 대부분의 연구는 semi-supervised 환경에서 task 들을 다루고 있다.
② Unsupervised training of GNNs
• GNN 의 비지도학습은 보통 mutual information 을 최대화 하는 방향으로 학습된다.
※ mutual information : 하나의 random variable 이 다른 random variable 에 얼마나 dependent 한지를 나타내는 지표로 P(X,Y) 가 P(X)P(Y) 와 얼마나 비슷한지를 측정한다. independent 관계라면 두 값이 같으며 MI 값은 0이 된다.
• 관련 연구 : Deep Graph Informax(2019), InfoGraph (2020)
③ Graph Pooling
• Graph Pooling 은 반복적인 data coarsening (범주를 간단화 시키는 것처럼 데이터를 함축시키는 것이라 생각하면 됨) 을 통해 그래프의 계층적 특징을 발견해내는 것이 목표
• 초기의 구조는 클러스터링 최적화 과정이 없는 고정된 axiomatic pooling 방식에 의존하다가 DiffPool (2018) 을 제안한 논문에서 처음으로 GNN 구조에서 학습가능한 풀링을 제안한 바가 있다.
• MinCutPool (2020) 을 제안한 연구에서는 풀링 전략으로서 spectral clustering 의 미분가능한 공식에 대해 소개한 바가 있다. MinCutPool 은 복잡한 그래프에서 주요한 노드를 추출하고자 한 여러 시도들 중 하나로 eigenvector 를 활용해야하는 spectral clustering 의 단점을 해소하면서 node feature 를 기반으로 클러스터링을 하는 방법론을 제시한다.
※ Spectral clustering : 그래프 기반의 클러스터링 기법으로, k-means clustering 과 같이 데이터 간의 거리를 기반으로 군집화를 진행하는 것이 아니라, 각 노드별로 연결이 되어있는지, 연결되어 있다면 얼마만큼의 강도로 연결되어 있는지를 중심으로 군집화를 진행하는 알고리즘에 해당한다.
👀 참고 : https://velog.io/@tobigs-gnn1213/5.-Spectral-Clustering#1-spectral-clustering-algorithms
5. Spectral Clustering
Spectral Clustering [작성자 : 정민준]
velog.io
👀 참고 : https://seungwooham.github.io/machine%20learning/MinCutPool1/
MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)
MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)
seungwooham.github.io
💡 Graph pooling 에 관한 properties
| End-to-End training | 종단학습은 그래프 구조와 노드 특성을 동시에 포착할 수 있도록 한다. |
| Unsupervised | 비지도학습은 클러스터링 모델링에 있어 desirable 한 학습방법이다. |
| Node aggregation | 클러스터링에서 graph pooling 을 해석하는데 있어 중요한 부분이다. |
| Sparse | 실제 그래프 데이터는 size 도 다양하며 sprsity 가 존재한다. |
| Soft aassignment | cluster 를 결정하는 것에 있어 soft 한 방식을 도입하면 클러스터 간 상호작용을 해석하는데에도 유연한 추론을 가능하게 한다. |
| Stable | 그래프 구조에 관하여, 클러스터링을 진행할 때 사용하는 함수는 stable 해야 한다. |
※ DMoN 은 subsampling 로 인한 정보의 손실 없이, Graph scalability 측면에서 가장 좋은 성능을 유지한다.
4️⃣ Preliminaries
① Notation
• V : set of nodes
• E : set of edges
• A : nxn adjacency matrix of G
• di : degree of vi
• F : graph partitioning function → V 를 k 개의 집단으로 분할하는 함수 (for data clustering)
• X : node attributes
② Graph Clustering Quality Functions
• DMoN 은 spectral 접근을 사용해 gradient 기반의 최적화 방식에 적합한 목적함수를 사용한다.
• spectral Clustering : Graph adjacency matrix 의 eigenvalue, eigenvector 를 사용해 클러스터링을 진행하는 방식
(1) Cut based metrics
👀 참고 : https://techblog-history-younghunjo1.tistory.com/93
[ML] Spectral Clustering(스펙트럴 클러스터링)
이번 포스팅에서는 클러스터링 모델 중 하나로서 스펙트럴 클러스터링에 대해서 소개하려 한다. 여기서 스펙트럴(Spectral) 자체는 행렬의 고윳값(Eigenvalue)을 의미한다. 이는 추후에 고윳값을 어
techblog-history-younghunjo1.tistory.com
👀 두 그룹으로 나누는 (Cut) 방식 2가지
• cut minimal (minimum cut) : 주어진 데이터들 사이의 유사도 값들 중 가장 작은 값으로 각각 클러스터로 나눈다. 첫번째 고유값은 보통 무의미한 해이기 때문에 두번째 고윳값부터 사용한다. (second eigenvector 를 사용하는 것과 비슷한 맥락)
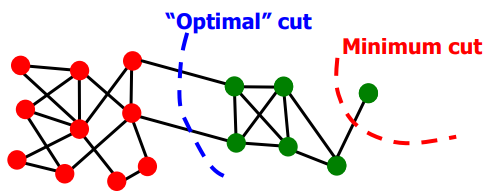
• ratio cut (normalized cut) : minimal cut 방법은 가중치 값이 작은 엣지가 클러스터 내부에 존재하게 된다면 분류가 잘못 이루어진다는 단점이 있다. 따라서 각 partition 의 total edge volume 을 이용해 normalized cut 방식을 도입한다. 보다 균형적인 partition 을 위해 MinCutPool 알고리즘에서도 normalized cut 방식을 도입한다.


(2) Modularity
• Modularity 목적함수는 "통계학적" 관점으로 클러스터링 문제를 접근하는 방법으로, 네트워크가 community 로 얼마나 잘 나누어졌는가에 대한 수치를 나타낸다. 랜덤한 그래프를 통해 얻어진 expectation 값을 기반으로 수치를 계산하는 null model 을 도입하여 클러스터링의 편차를 수량화 한다.
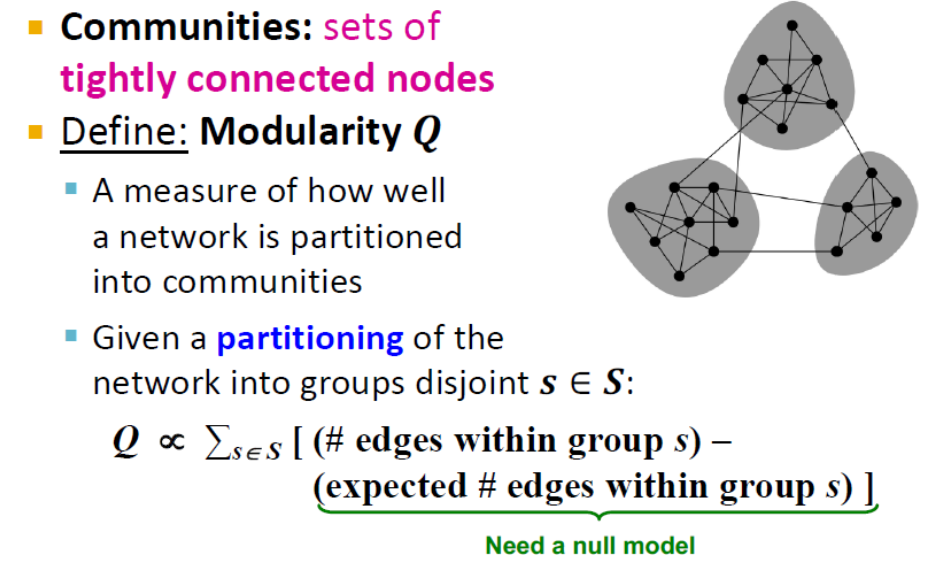
🔹 Modularity measure

↪ Fully Random Graph with given degrees, node u and v with degrees d(u) and d(v) are connected with probability d(u)◦d(v)/2m
↪ n is # of nodes and m is # of edges
Undirected Graph 라고 가정했을 때, 모든 엣지는 2번씩 세어질 수 있고, 따라서 이때의 d(v)/2m 은 특정 노드가 노드 v 와 연결될 확률로 볼 수 있으며 (가능한 전체 엣지의 개수 분에 v 에 연결된 엣지의 개수), multi-graph (두 노드 사이에 엣지의 개수가 여러 개 형성될 수 있는 그래프) 이므로 노드 u 의 차수를 곱해주면 노드 u 와 v 사이에 기대할 수 있는 엣지의 개수가 도출되는 것이다.
Modularity 는 실제 두 노드 사이의 엣지 개수를 의미하는 Aij 와 그 기댓값의 차이를 계산함으로써 결과가 얻어지며, Normalizing 을 위해 2m 을 나누어줌으로써 -1과 1사이의 값을 갖게 된다. 이때 값이 음수를 가지면, Aij < didj/2m 으로 연결될 것으로 기대한 엣지 갯수보다 실제 연결된 경우가 더 작은 것으로 노드 u와 v 가 속한 cluster 는 week group 이라 볼 수 있다. 반면 1에 가까운 양수값을 가진다면, 평균적인 연결보다 더 많은 엣지의 연결이 이루어진 것이기에 해당 cluster 는 strong group 이라 해석해볼 수 있다.
• Modularity metric 은 graph clustering metric 으로 가장 자주 유용하게 사용되는 지표에 해당한다.
③ Spectral Modularity Maximization
Modularity 를 최대화 하는 것은, 그래프 내에 엣지를 전부 비교해야 하기 때문에 다항시간 내에 풀 수 없는 NP-hard 문제를 가지게 된다. 따라서 효율적으로 계산하기 위해 eigenvector 를 통해 분할하는 방법인 Spectral modularity 방법을 고안하게 된다.

▸ C : cluster assignment matrix (nxk) , k is # of clusters
▸ d : degree vector
▸ B : modularity matrix, B = A - dd' / 2m , A is adjacency matrix
Modularity 를 최대화 하면서 Optimal 한 C 는 modularity matrix B 의 Top-k eigenvector 이다.
※ eigenvalue, eigenvector

5️⃣ Method
① DMoN : Deep Modularity Networks
• attributed graph clustering with GNN
↪ Propse fully differentiable unsupervised clustering objective which optimize soft cluster assignments
↪ Propse collapse regularization method
• DMoN architecture 의 핵심요소 2가지
(1) cluster assignments C 를 encode 하는 것


소프트맥스 함수를 통과시켜 인코딩 함으로써 미분 가능하게 만든다. soft 한 방식의 클러스터 할당을 위해 Graph Convolutional Network 를 사용한다. A' 는 normalized adjacency matrix (정규화된 인접행렬) 를 의미하며 X 는 node attributes (node features) 를 의미한다. (n x s). D 는 A 의 degree matrix 를 의미한다.
(2) C 를 최적화하는 objective function

→ ( spectral modularity maximization + collapse reularization ) 이때 정칙화 부분을 추가한 이유는 최적화 때문!
▸ B : modularity matrix (nxn), C : cluster assignment matrix (nxk), A : adjacency matrix (nxn)

▸ Frobenius norm (Uclidean norm) 방식으로 L2 norm 정칙화와 비슷한 형태를 띈다.

▸ Tr( ) 수식은 행렬 A 의 대각 요소들을 모두 더하는 연산을 의미한다.
② Collapse Regularization
• spectral clustering 의 단점을 극복해서 나온 그래프 클러스터링 기법이 MinCutPool
MinCutPool 의 objective function 은 두 가지 손실함수로 이루어져 있는데, 첫번째는 Cut loss Lc 이고 두번째는 Orthogonality loss Lo 이다. Lc 의 수식은 'cluster 내부의 연결성' / 'graph 전체의 연결성' 으로 그래프 전체의 연결성과 비교해 해당 클러스터 내부가 얼마나 강하게 연결되어 있는지 알려준다. 강하게 연결되어있는 노드들이 서로 함께 cluster 가 되도록 한다. Cut loss 만 고려하게 된다면 node feature 를 uniform 하게 만들어 local minima 에 빠질 위험이 높아진다. 따라서 Lo 를 도입하는데, 이를통해 클러스터 할당이 orthogonal 하도록 하여 모든 노드가 모든 클러스터에 같은 정도로 속하는 문제를 해결하고, 클러스터의 크기가 비슷하도록 유도한다.
본 논문에서는 MinCutPool 의 soft-orthogonality regularization 이 softmax class assignment 와 결합되었을 때, C 값의 범주를 완전히 제한하여 loss 를 증가시키는 문제를 제기한다.
CORA dataset (논문 DB) 에 대해 200 epoch 의 training 을 진행하였을 때, Orthogonality regularization term 이 MinCutPool 의 최적화를 좌우하여 objective function 이 제대로 동작하지 못하고 있음을 보여준다.
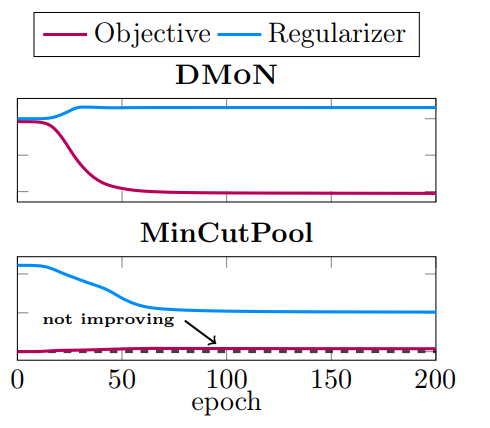

클러스터링 과정에서 MinCutPool objective function (joint optimization) 을 사용했을 때와 단순히 feature orthogonalization 을 했을 때를 비교한 결과이다. 5개의 dataset 에서 3개의 경우가 orthogonality 만을 사용했을 때 label correlation 이 더 좋았다. 이처럼 Regularization term 은 자칫하다 성능을 좌우할 수 있음을 보여주고 있다.
따라서 DMoN 은 MinCutPool 의 Lc + Lo joint optimization 방식이 아닌, collapse regularization 방법을 도입해, Regularization 문제를 해결하고자 한다. 이를통해 목적함수의 최적화를 효과적으로 진행시킬 수 있도록 한다.
③ Theoretical insights
• 제안한 objective function 의 타당성을 입증하기 위해, 특히 새롭게 제시하는 'collapse regularization' 방식에 대한 설명을 위해 정리한 이론과 증명을 제시한다.
(1) 첫번째 이론

✨ cluster assignments matrix C 가 positive modularity 를 가진다면, objective score L(DMoN) 은 값이 더 작아질 것이다. (smaller loss)
(2) 두번째 이론 (그래프 클러스터링 알고리즘의 일관성 consistency 에 관한 내용을 소개)

↪ λn : average degree of the network (n 표기는 특정 노드를 의미함)
clustering 알고리즘이 consistent 하다는 것은 error rate 을 vanishing 하게 만든다는 뜻이며, compatiable 호환 가능한 목적함수는 이러한 일관성의 특징을 가지고 있다. DMoN 은 collapse constraints part 를 도입하더라도 일관적인 prediction 성능을 유지한다.
6️⃣ Experiments
👀 코드 : https://github.com/google-research/google-research/tree/master/graph_embedding/dmon
GitHub - google-research/google-research: Google Research
Google Research. Contribute to google-research/google-research development by creating an account on GitHub.
github.com
synthetic data (인위적으로 생성한 데이터) 와 real-world data 데이터셋을 활용해 실험을 진행하였으며, 평가지표로는 graph clustering 에 관한 지표와 label alignment 에 관련한 지표를 사용하였다.
🔹 Datasets
▢ Synthetic data

▢ Real datasets

• |X| : node feature , |Y| : labels
• Cora, Citeseer, Pubmed → Citation network
| 노드 | 엣지 | features | labels |
| papars | citation | bag of words of abstracts | papaer topics |
• Amazon PC, Photo → subsets of Amazon co-purchase graph for the pc and photo sections of the web
| 노드 | 엣지 | features | labels |
| goods | frequently purchased together | bag of words of reviews | product catecory |
• Coauthor CS, Coauthor Phys, Coauthor Med, Coauthor Chem, and Coauthor Eng → co-authorship networks
| 노드 | 엣지 | features | labels |
| authors | co-authored | collection of paper keywords | most common fields of study |
🔹 Baselines
그래프 구조 혹은 노드 속성에 대한 정보를 이용하여 클러스터링을 할 수 있는 baseline model 을 사용함


※ SBM : 특정 노드끼리 community structure 을 가지는 그래프를 만들 수 있는 generative model
각 베이스라인 모델에 대하여, 기본적인 GNN 모델구조는 one hidden layer with 512 neurons for real world datasets and 64 neurons for synthetic datasets 로 고정하고 최대 16개의 cluster 로 할당할 수 있도록 setting 을 진행한 다음, Parameter tuning (e.g # of random walks, window size, loss coefficient, dropout...) 을 진행했다.
🔹 Metrics
• graph based clustering metrics : graph modularity (값이 클수록 좋음), average cluster conductance (값이 작을수록 잘 형성된 클러스터라 볼 수 있음)
• label based metrics : normalized mutual information (값이 클수록 좋음), pairwise F1 score

⁕ cf) 모든 지표값에 100을 곱하여 성능 비교를 진행함
🔹 Results
(1) Synthetic data

(2) Real world data


👉 굵은 활자가 가장 best score 를 보인 부분이라 볼 수 있음
7️⃣ Conclusions
① DMoN 은 attributed graph clustering 알고리즘으로, unsupervised objective 함수를 사용해 훈련을 진행한다.
② DMoN 은 graph 구조와 node feature 를 모두 고려하여 훈련을 진행할 수 있으며, synthetic data 와 real world data 에서 모두 baseline model 보다 좋은 성능을 보였다.
'3️⃣ Study at Univ > ○ 논문읽기' 카테고리의 다른 글
| [Causal Forest] 머신러닝 기반의 인과 포레스트 기법을 활용한 처치효과 검증: 교내 동아리활동 참여가 협업능력에 미치는 효과를 중심으로 (1) | 2024.01.23 |
|---|---|
| [DiD, Matching] Popularity or Proximity (0) | 2023.07.02 |
| DeepWalk (1) | 2022.11.03 |
| 앱 리뷰 분석에 관한 논문 정리 ③ (0) | 2022.06.16 |
| 앱 리뷰 분석에 관한 논문 정리 ② (0) | 2022.06.15 |




댓글