📌 3장. 통계기법의 이해
⭐ 기술통계학 : 자료의 수집 정리 및 요약 해석을 통해 모수를 규명
⭐ 추론 통계학 : 기술통계로 얻은 통계량을 기초로 모수를 추론하고 검정한다.
1️⃣ 기술통계
(1) 표본추출
a. 표본조사
- 대상집단의 일부를 표본으로 하는 조사
b. 용어정리
- 모집단 : 조사하고자 하는 대상 집단 전체
- 원소 : 모집단을 구성하는 개체
- 표본 : 조사하기 위해 뽑은 모집단의 일부 원소
- 모수 : 표본관측에 의해 구하고자 하는 정보
- 표집틀 : 표본추출시 필요한 모집단의 구성요소와 표본 추출 단계별로 표본추출단위가 수록된 목록
c. 표본 추출 과정
- 모집단 결정 👉 표집틀 선정 👉 표본 추출 방법 결정 👉 표본크기 결정 👉 표본 추출
- 표집틀은 모집단의 구성 요소를 모두 포함하는 반면 각각의 요소가 이중으로 포함되지 않도록 한다.
- 표본추출 방법에는 크게 확률 표본추출방법과 비확률 표본추출방법이 있다.
d. 표본추출 방법 ⭐⭐
- 모집단에 속한 모든 원소들이 표본으로 뽑힐 가능성 여부에 따라 2가지 방법으로 구분한다.
| 기준 | 확률표본추출 | 비확률표본추출 |
| 연구대상이 표본으로 추출될 확률 | 동등함, 알려져 있을때 | 동등하지 않음, 알려져있지 않음 |
| 표본추출 | 무작위적 | 인위적 |
| 표본의 통계치로 모수 추정 | bias 가 없음 | bias가 있음 |
| 모수 추정 가능성 | 추정 가능 | 추정 불가능 |
| 오차 측정 가능성 | 측정 가능 | 측정 불가능 |
| 시간과 비용 | 많이 소요됨 | 적게 소요됨 |
| 모집단의 규모와 성격 | 명확히 규정 | 불명확 or 불가능 |
🔹 확률 표본 추출법
- 표집틀을 이용해 모집단으로부터 동일한 확률로 표본의 원소들을 추출하는 방법
- 때문에 속성 측면에서 모집단을 대표할 우수한 표본을 추출할 가능성이 높다.
- 무작위 표본추출이기 때문에 시간과 비용이 많이 든다는 제약
- 단순랜덤 추출법 random : n 개의 표본이 추출된 가능성을 동일하게 해주는 방법. 난수표를 통해 표본을 뽑을 수 있으나 모집단이 매우 크면 현실적인 어려움이 있다.
- 계통 추출법 Systematic : 단순 랜덤 추출법의 변형된 방식으로, 번호를 부여한 샘플을 나열해 K 개씩 n 개의 구간으로 나누어 매번 k 번째 떨어진 간격에 위치하는 원소들을 표본으로 추출하는 방법. 단순하고 편리해 많이 사용됨
- 집락 추출법 Cluster : 모집단이 몇 개의 집단이 결합된 형태로 되어있고, 각 집단 내부에서 원소들에게 일련의 번호를 부여할 수 있을 때 이용되는 방법. 일부 집단을 랜덤으로 선택하고 각 집단 내에서 표본을 임의로 선택하는 방법
- 집단 내 → 이질적, 집단 간 → 동질적
- 층화 추출법 Stratified : 이질적인 원소들로 구성된 모집단에서 각 계층을 고루 대표할 표본을 추출하는 방법
- 집단 내 → 동질적, 집단 간 → 이질적
🔹 비확률 표본 추출법
- 랜덤하게 추출하지 않는 방법을 포괄적으로 의미
- 분석 결과의 일반화에 제약이 있다.
- 비용이 적게들고 실행하기 쉽다는 장점이 있고, 표집틀을 구할 수 없는 상황에서는 이 방법이 사용됨. 현실적으로 확률 표본추출법보다 더 많이 사용된다.
- 편의 표본추출 Convenient : 정해진 크기의 표본을 선정할 때까지 조사자 임의대로 원소들을 표집. 추출된 표본엔 조사자의 편견이 삽입되어 있지만 가장 자주 사용되는 방법이다.
- ex. 학교에서 나오는 사람들을 대상으로 설문
- 유의 표본추출 Judgemental : 연구자의 의도 또는 판단에 따라 전형적인 대상을 표본으로 추출하는 방법
- ex. 정당이 과거 선거결과를 잘 대표한 적당한 선거구를 표본으로 추출
- 지원자 표본추출 Volunteer : 메일이나 광고지 등을 통해 연구를 광고한 뒤 참가 희망자들을 대상으로 표본 추출
- ex. 약물 임상시험
- 할당 표본추출 Quota : 각 속성의 구성 비율을 고려해 표본을 추출하는 방식. 외견상 층화 표본추출과 매우 비슷하나 표집틀이 없다는 차이가 있다.
- ex. 1학년 200명, 2학년 100명, 3학년 500명에서 각각 20명, 30명, 40명을 임의 추출
- 눈덩이 표본추출 Snowball : 소수 참여 대상자로부터 또 다른 참여 대상자를 계속적으로 소개받는식으로 표본을 누적. 네트워크 표본추출
- ex. 병원종사자 간 환자 의료정보 공유 방법 등에 대한 연구
(2) 데이터 요약
a. 그래프 표현, 숫자 요약
- 이산형 : 막대그래프, 원그래프
- 연속형 : 히스토그램, 줄기잎그림, 상자그림, 산포도, 선그래프
- 중심경향도, 산포도, 비대칭정도 등 기술통계 활용
b. 자료의 측정과 형태 ⭐⭐
- 측정 Measurement : 표본으로 추출된 원소들로부터 주어진 목적에 적합하도록 관측하기 위해 자료를 얻는 방법
| 이산형자료 (질적자료) | 명목척도 | 측정 대상이 어느 집단에 속하는가에 사용되는 척도 - 성별, 출생지, 직업 |
| 순서척도 | 서열관계를 관측하는 척도 - 선호도, 학력, 연령대 |
|
| 연속형 자료 (양적자료) | 구간척도 | 속성의 양을 측정. 절대적인 원점이 존재하지 않음 - 온도, 지수 등 |
| 비율척도 | 절대적인 원점이 존재. 두 측정값의 비율이 의미가 있음 - 무게, 나이, 시간, 거리 |
(3) 확률분포
a. 확률 👉 전공자라 아는 내용 PASS
b. 확률변수
🔹 이산형 확률변수 , 확률질량변수
🔹 연속형 확률변수 , 확률밀도함수
🔹 누적분포함수
c. 확률분포
🔹 이산형 확률분포 ⭐⭐
- 베르누이 확률분포 : 결과가 2개만 나오는 경우. 평균 = p, 분산 = p(1-p) , p 는 성공확률 ⭐
- 이항분포 : 베르누이 시행을 n번 반복했을 때 k 번 성공할 확률. 평균 = np, 분산 = np*(1-p) ⭐
- n 이 충분히 크면 이항분포는 정규분포에 가까워진다.
- 성공확률 p 가 1/2에 가까우면 종모양이 된다.
- 기하분포 : 성공확률이 p 인 베르누이 시행에서 처음 성공이 일어날때까지 반복한 시행횟수를 X 라 할때 X는 성공확률이 p 인 기하분포를 따른다고 한다. X ~ Geo(p). 평균 = 1/p, 분산 = (1-p)/p^2
- 다항분포 : 이항분포의 확장버전. 세가지 이상의 결과를 가지는 반복시행에서 발생하는 확률분포
- 포아송분포 : 시간과 공간 내에 발생하는 사건의 발생횟수에 대한 확률분포
- lambda : 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기대값, y = 사건이 일어난 수
- 평균 = 분산 = lambda
🔹 연속형 확률분포 ⭐⭐
- 균일분포 : 확률밀도함수의 값이 모두 동일한 확률분포
- 정규분포 ⭐ : 평균이 mu, 표준편차가 sigma 인 x의 확률밀도함수로 좌우대칭의 종모양
- 표준정규분포 : 평균이 0이고 분산이 1인 분포
- 표준화 Z = (X-mu)/sigma
- 지수분포 : 어떤 사건이 발생할 때까지 경과시간에 대한 연속활률분포로 지속시간과 관련된 현상을 나타내는데 유용한 함수
- ex. 제품의 수명에 대한 분포
- 단위시간당 사건의 발생이 포아송 분포를 따른다면, 한 사건이 일어난 후 다음 사건이 일어날 때까지의 시간은 지수분포를 따른다.
- t 분포 ⭐
- 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포를 따른다. 신뢰구간과 가설검정에서 사용되는 분포이다.
- 표본이 크면 자유도가 증가해 표준정규분포와 비슷한 형태
- 모표준편차를 모르며 표본의 크기가 30보다 작고 집단 간 평균이 동일한지 알고자 할 때 사용한다.
- 자유도 = n-1
- 감마분포의 일종인 분포이다.
- 표준정규분포를 따르는 변수와 카이제곱분포를 따르는 변수의 비율 형태로 표현되는 변수
- 카이제곱 분포
- 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설검정에 사용되는 분포이다.
- 두 집단의 동질성 검정에 활용된다.
- 카이제곱분포는 분산의 특징을 나타낸 분포로 그래프 상에서 양의 값만 존재하고 오른쪽으로 꼬리가 긴 비대칭 분포의 형태를 가진다.
- 자유도가 커지면 분포의 모양이 대칭에 가까워진다.
- 표준정규분포를 따르는 변수의 제곱합에 대한 분포이다.
- 자유도 = n-1
- 왼쪽의 확률 : 1-alpha, 오른쪽의 확률 : alpha
- F 분포 ⭐
- 두 집단간 분산의 동일성 검정에서 사용되는 검정 통계량의 분포
- 비대칭 분포로 두 개의 자유도 n1 분자 , n2 분모 에 의해 분포 형태가 결정된다. 분산이 큰 집단이 분자에 위치한다.
- 확률변수는 항상 양의 값만 가지고 자유도를 2개 가지고 있으며 자유도가 커질수록 정규분포형태에 가까워진다.
- 신뢰구간과 가설검정, 분산분석에 사용하는 분포이다.
- 서로다른 카이제곱분포의 비율 형태로 표현되는 분포
(4) 표본분포
a. 확률표본
- 확률변수 X가 특정 확률분포를 따른다 할 때, 이 확률분포로부터 독립적으로 관측된 n 개의 표본을 뜻한다. (X1,X2,...,Xn) 상호 독립적인 관계이며 각 X 는 동일한 분포를 가진다.
- 확률변수의 함수로 정의된 통계량도 또한 확률변수이다.
- 모수를 추정하는 통계량을 추정량이라하며 구체적인 표본에 근거해 구한 추정량의 값을 추정치라 한다.
b. 표본분포
- 비표본오차 : 표본오차를 제외한 조사 전체 과정에서 발생가능한 오차
- 표본오차 : 모집단의 전체 특성을 표본으로 추론함으로써 생기는 오차
- 표준오차 : 표본분포의 표준편차
- 표본 평균의 분포 : 표본 평균의 기대값은 모평균과 일치하고, 표본평균의 표준오차는 모표준편차를 sqrt(n) 으로 나눈 것이다.
c. 중심극한정리
- 모집단의 분포가 실제로 정규분포가아닌 경우에도 중심극한정리에 의해 정규분포를 이용한 추정량의 근사확률을 구할 수 있다.
- n 이 커질수록 표본평균의 분포가 정규분포에 가까운 분포를 가진다는 의미
2️⃣ 추론통계
⭐ 용어 묻는 문제
- 모집단의 특성을 추측하는 통계 기법
- 추정 : 모수가 무엇일까를 추측
- 가설검정 : 가설을 설정한 후 그 가설이 옳은지를 판단하여 가설의 채택여부를 결정
(1) 점추정
모수에 대한 특정 값을 지정
a. 모평균의 추정량 : 표본평균, 중앙값, 최소값, 최대값, 최솟값, 최소값과 최대값의 평균
- 추정량도 특정한 확률분포를 갖는다. (확률표본에 있는 확률변수의 함수 이므로)
- 불편성 : 추정량의 분포의 중심이 추정하고자 하는 모수이다.
- 효율성 : 추정량의 분포의 흩어진 정도가 작은 추정량 (분산이 작을수록 좋다)
- 불편성과 효율성을 만족하는 추정량을 최소분산불편추정량 이라고 한다.
- 일치성 : 표본의 크기가 아주 커지면 추정량이 모수와 거의 같아진다.
- 충족성 : 추정량은 모수에 대해 모든 정보를 제공한다.
- 표본평균 : 모집단의 평균을 추정하기 위한 추정량으로 확률분포의 평균값
- 표본분산 : 모집단의 분산(모분산)을 췆ㅇ하기 위한 추정량
- 모분산의 추정량
- 표본분산 S^2 는 모분산의 불편추정량이나 최소분산을 갖는 추정량은 아니다.
- 분모가 (n-1) 임에 주의하기 (n 으로 나누면 최소분산을 갖는 추정량이 된다)
- 모비율의 추정량
(2) 구간추정
- 확률로 표현된 믿음의 정도 하에 모수가 특정한 구간에 있을 것이라고 선언하는것
- 신뢰수준 : 구해진 구간 안에 모수가 있을 가능성의 크기로, 일반적으로 90%, 95%, 99% 의 확률을 이용하는 겨우가 많다.
- 신뢰구간 : 각각의 신뢰수준 하에서 모수가 존재할 것이라고 구한 구간
a. 단일 모수의 신뢰구간 추정
🔹 모평균의 신뢰구간 : 모평균의 추정량은 표본평균이다. 모평균의 구간 추정은 모분산이 알려져있느냐의 여부에 따라 케이스가 나뉘어진다.
- 모분산이 알려져있는 경우 : Xbar +- Z * sigma/sqrt(n)
- 90% 👉 Z = 1.645, 95% 👉 Z = 1.96 , 99% 👉 Z = 2.57
- 모분산을 모르는 경우
- n > 30 인 경우 : Xbar +- Z * S/sqrt(n)
- n <= 30 인 경우 : Xbar +- t * S/sqrt(n)
🔹 모비율 P 의 신뢰구간 : 모비율 P의 추정량은 표본비율이다.
- 평균은 P, 분산은 1/n * P * (1-P) 이며 중심극한 정리에 의해 표준정규분포가 된다.
- P +- Z* sqrt( P(1-P) * n )
🔹 모분산의 신뢰구간 : 모분산의 추정량은 표본분산 S^2 이다.
- 표본분산 S^2 의 표본분포는 자유도가 (n-1) 인 카이제곱분포가 된다.
- (n-1)*S^2 / 카이제곱
b. 서로 독립인 두 모집단으로부터 두 모수의 차이에 대한 추정
- 두 모수의 차이에 대한 추정은 두 집단이 서로 독립이라는 전제조건이 필요하다.
🔹 두 모평균의 차이의 신뢰구간
- 평균 : Mu1 - Mu2
- 표준편차(표준오차) 👉 모분산을 알고있는 경우에 따라 구분
- 모두 모분산을 아는 경우
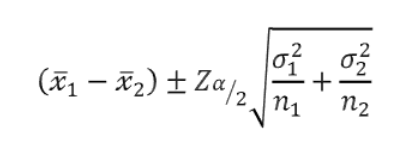
- 모두 모분산을 모르는 경우 & 대표본 (n>=30)
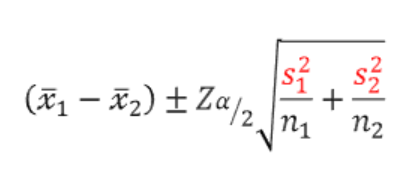
- 모두 모분산을 모르는 경우 & 소표본 : 두 모집단의 통합분산을 사용
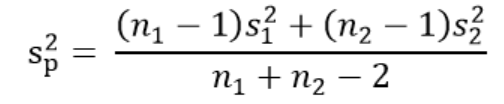
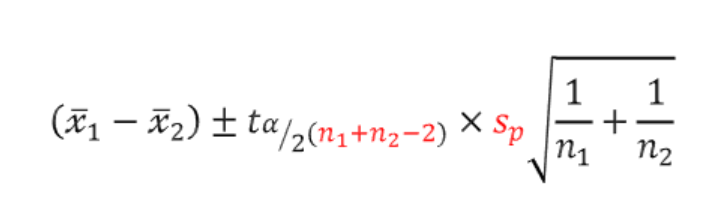
🔹 서로 독립이 아닌 두 모집단 사이 모평균 차이 추정
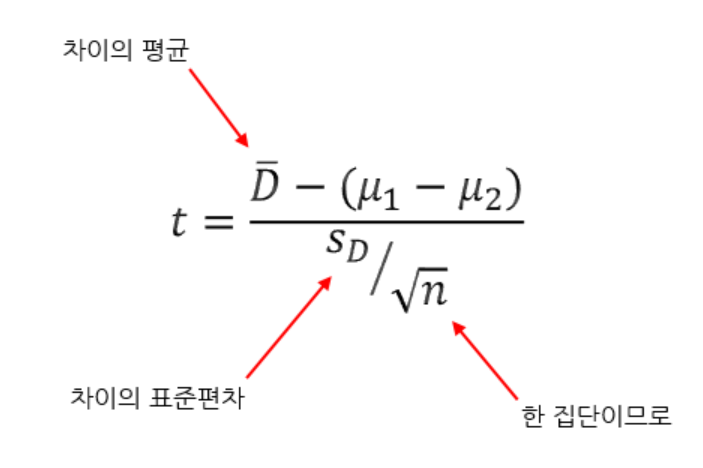
- 대응표본의 두 모평균 차이의 신뢰구간
- 대응표본 : 투약 전후나 이벤트 성과 비교와 같이 짝을 이루는 각 쌍에 대한 표본을 대상으로 하는 경우
- di : 짝을 이룬 n 개의 표본들의 차이
- 자유도 (n-1) 의 t 분포를 이용한다. 이때 두 모집단은 정규분포를 따른다는 전제는 필요하다.
🔹 두 모비율 차이 P1-P2 의 신뢰구간
- 두 표본이 모두 독립표본이고 np>=5, n*(1-p) >=5 라는 전제가 필요하다. 이 조건이 만족되면 두 표본비율의 차이가 정규분포를 따른다.
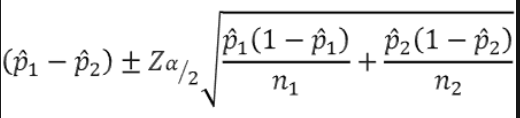
🔹 두 모분산 비율의 신로구간
- 두 모분산 비율의 추정량은 두 표본분산의 비율이다.
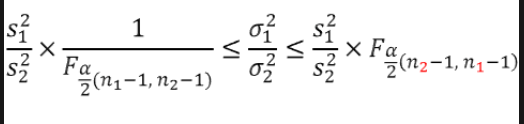
- 큰 표본분산은 항상 분자에 놓음으로써 두 모분산의 비율이 1보다 크게 항상 설정한다.
(3) 최대 우도 추정법
a. MLE
- MLE : 모수가 미지의 θ인 확률분포에서 뽑은 표본 x들을 바탕으로 θ를 추정하는 기법
- Likelihood 우도 : 이미 주어진 표본 x들에 비추어 볼 때 모집단의 모수에 대한 추정이 그럴듯한 정도
b. 우도 함수
- 확률밀도함수 또는 확률질량함수 : P(x;θ) 👉 θ 는 이미 알고있는 상수계수이고 x가 변수이다. 함수의 전체 면적은 항상 1이다.
- 우도함수는 확률밀도함수에서 θ를 변수로 보는 경우에 해당한다. L(θ;x) 로 표기한다. 함수의 전체 면적이 항상 1이 되는 것은 아니다.
c. 로그 우도 함수
- 수치적 최적화를 위해 일반적으로 우도를 직접 사용하지 않고 로그 변환한 로그-우도함수를 많이 사용한다.
- 로그는 단조증가함수이기 때문에 L(θ)를 최대화 하는 세타는 logL(θ) 에서도 최대이다.
d. 최대 우도 추정법
- 로그-우도를 최대화 하는 파마리터 θ를 추정하는 방법이다.
- 주어진 표본에 대해 우도를 가장 크게하는 모수를 찾는 방법 θmle 로 표기한다.
e. 분포별 MLE
- 베르누이 분포 (p) : Xbar (표본평균)
- 기하분포 (p) : 1/Xbar
- 포아송 분포 (lambda) : Xbar
- 정규분포
- 모평균 : Xbar
- 모분산 : 1/n * Σ(xi-xbar)^2
- 지수분포 : Xbar
(4) 가설검정
- 모집단의 모수 추정 이후 모집단에 대해 가설을 설정하고 그 가설의 타당성 여부를 검정하는 것
- 가설은 모수 (모평균, 모분산, 모비율) 에 대하여 설정한다.
- 가설검정의 단계
귀무가설, 대립가설 설정 👉 검정 통계량의 분포를 구한다 👉 유의수준을 결정하고 검정통계량의 분포에서 기각역 C 를 결정한다 👉 귀무가설이 옳다는 전제 하에서 검정통계량의 값을 구한다 👉 기각역 C 에 검정통계량이 속하는가를 판단해 기각 여부를 결정한다.
a. 가설
- 귀무가설과 대립가설을 설정한다.
- 귀무가설 : 비교하는 값과 차이가 없다. 동일하다.
- 대립가설 : 뚜렷한 증거가 있을 때 주장하는 가설
b. 검정통계량
- 가설검정에서 관찰된 표본으로부터 구하는 통계량으로 분포가 가설에서 주어지는 모수에 의존한다.
- 귀무가설이 항상 옳다는 전체하에서 구한 검정통계량의 값이 나타날 가능성이 크면 H0 를 채택, 아니면 기각
c. 유의수준 α
- 귀무가설 H0 가 옳은데도 불구하고 이를 기각하는 확률의 크기
- 일반적으로 0.01, 0.05, 0.1 을 설정한다.
- 구간추정에서 (1-α)*100% 신뢰구간의 α 가 바로 가설검정의 유의수준을 의미한다.
d. 기각역
- 검정통계량의 분포에서 확률이 유의수준 α 인 부분
e. P 값
- 유의확률
- 귀무가설에 대한 기각 기준을 삼고 관측되는 확률값으로 귀무가설의 기각이 가능한 최소 유의수준 확률
- 귀무가설을 얼마나 지지하는지를 나타낸 확률
- p 값이 유의수준 α 보다 작은 경우에 귀무가설을 기각한다.
f. 대립가설 H1 과 기각역 C
- 유의수준에 의해 기각역의 크기가 결정된다.
- 양측검정 : 모수가 특정값이 아니다 (=/) 라고 할 때 대립가설이 주어지는 경우 : α/2
- 왼쪽 단측검정 : 모수가 특정값보다 작다라고 대립가설이 주어지는 경우
- 오른쪽 단측검정 : 모수가 특정값보다 크다라고 대립가설이 주어지는 경우
g. 제 1종오류, 제 2종 오류 ⭐⭐
- 제 1종 오류 α : 귀무가설이 옳은데도 불구하고 H0 를 기각하는 오류의 크기
- 제 2종 오류 β : H0 가 옳지 않은데도 불구하고 H0 를 채택하는 오류
- α 와 β는 상충 관계에 있다. 알파가 감소하면 베타가 증가한다.
(5) 통계분석 방법론
| 가설검정 | |||
| 평균검정 , 분산검정 | |||
| t검정 | 분산분석 | 카이제곱검정 | F검정 |
| - 단일 표본 검정(모집단 1개) - 독립표본 검정 (모집단 2개) - 대응표본 검정 (모집단 전후) |
모집단 2개 이상 | 모집단 1개 | 모집단 2개 |
* 단일표본 t검정 : 하나의 모집단에 대한 가설점정 ⭐⭐
* 독립표본 t검정 : 두 집단이 서로 독립적일 때 두 집단간 평균차이 검정 ⭐⭐
* 대응표본 t검정 : 동일한 모집단에 변수를 노출시키기 전과 후의 평균값 비교검정 ⭐⭐
a. 단일 모수의 검정 (t검정)
🔹 모평균의 t 검정
- 종속변수는 연속형 변수여야하며 검증하고자 하는 기준값이 있어야 한다.
- 가설설정 👉 유의수준 설정 👉 검정 통계량의 값 및 유의확률 계산 👉 기각여부판단 및 의사결정
b. 대응표본 t 검정
- 단일 모집단에 대해 두 번 처리를 가할때 두 개의 처리에 따른 평균의 차이를 비교하고자 할 때 사용하는 검정 방법이다.
- ex. 판매사원들에게 두 가지 교육방법으로 직업교육을 하고나서 두 방법에 따른 판매실적 평균의 차이 확인
- 모집단과 표본은 하나씩이지만 각 개체별로 두 개의 값이 쌍으로 이루어져 있으므로 모수는 2개다.
- 모집단의 관측값이 정규성을 만족해야하며 종속변수가 연속형 변수여야 한다.
- 모수 : 두 개의 모평균 사이의 차이 D
- 귀무가설 : 두 개의 모평균 간에는 차이가 없다.
- 대립가설 : 차이가 있다. (양측검정)
c. 독립표본 t 검정
- 두 개의 독립된 모집단의 평균을 비교
- 정규성, 독립성, 등분산성 (분산이 서로 같음, 등분산 검정을 먼저 해야함 → 만족 여부에 따라 다른 계산 방법을 사용한다. ) 만족
- 독립변수는 범주형, 종속변수는 연속형이여야 한다.
- ex. 성별에 따라 출근시간 준비의 차이
- 양측검정, 단측검정
- 가설설정 👉 유의 수준 설정 👉 등분산 검정 👉 검정통계량의 값 및 유의확률 계산 👉 귀무가설의 기각여부 판단 및 의사결정
- 등분산 검정 결과에 따라 표준편차 계산 방식이 달라진다.
3️⃣ 분산분석 ⭐⭐
- t 검정이 두 집단 간의 평균 차이를 비교하는 방법이라면 분산분석은 두 개 이상의 다수 집단 간 평균을 비교하는 분석 방법이다. (분산 차이가 아님을 주의하기)
(1) 일원배치 분산분석 ANOVA
a. 분산분석
- 두 개 이상의 집단에서 그룹 평균 간 차이를 그룹내 변동에 비교하여 살펴보는 통계 분석 방법
- 두 개 이상의 집단들의 평균 간 차이에 대한 통계적 유의성을 검증
| 분석구분 | 명칭 | 독립변수 개수 | 종속변수 개수 |
| 단일변량 분산분석 | 일원배치 분산분석 | 1개 | 1개 |
| 이원배치 분산분석 | 2개 | ||
| 다원배치 분산분석 | 3개 이상 | ||
| 다변량 분산분석 | MANOVA | 1개 이상 | 2개 이상 |
b. 일원배치 분산분석 개념
- 반응값에 대한 하나의 범주형 변수의 영향을 알아보기 위해 사용되는 검증방법
- 모집단의 수에 제한이 없고 표본의 수가 같지 않아도 된다.
- F 검정 통계량을 사용한다.
c. 가정
- 각 집단의 측정치는 서로 독립적이며 정규분포를 따른다.
- 각 집단의 측정치의 분산은 같다.
d. 분산 분석표
| 요인 | 제곱합 SS | df 자유도 | 평균제곱 | 분산비 F |
| 처리 | SSA | k-1 | MSA | F = MSA/MSE |
| 오차 | SSE | N-k | MSE | |
| 전체 | SST | N-1 |
* k 는 집단의 수, N 은 관측의 수
* SSA : 집단이 가지는 변동제곱합
* SSE : 오차가 가지는 변동제곱합
* SST : 관측치 값이 가지는 변동제곱합
e. 가설검정
- H0 : k 개의 집단간 모평균에는 차이가 없다.
- H1 : k 개의 집단간 모평균이 '모두 같다고는 할 수 없다'
f. 사후검정
- H0 가 기각되었을 때 적어도 한 집단에서 평균의 차이가 있음을 통계적으로 증명되었을 경우, 어떤 집단에 대해 차이가 존재하는지 알아보기 위해 실시하는 분석
- 던칸의 MRt, 피셔의 LSD 방법, 튜키의 HSD 방법, Scheffe 방법 등이 있다.
(2) 이원배치 분산분석 ⭐ - 교호작용
a. 개념
- 반응값에 대해 두 개의 범주형 변수 A, B 의 영향을 알아보기 위해 사용되는 검증
- ex. 성별과 학년에 따른 시험점수의 차이
- 두 독립변수 A 와 B 사이에 상관관계가 있는지를 살펴보는 교호작용에 대한 검정이 반드시 진행되어야 한다.
b. 가정
- 정규성
- 등분산성
c. 주효과와 교호작용효과
- 주효과 : 각각의 독립변수가 종속변수에 미치는 효과
- 교호작용 : 두 독립변수의 범주들의 조합으로 인해 종속변수에 미치는 특별한 영향
- 두 독립변수 A, B 사이에 상관관계가 존재하는 경우 교호작용이 있다고 판단한다.
- 분산분석표
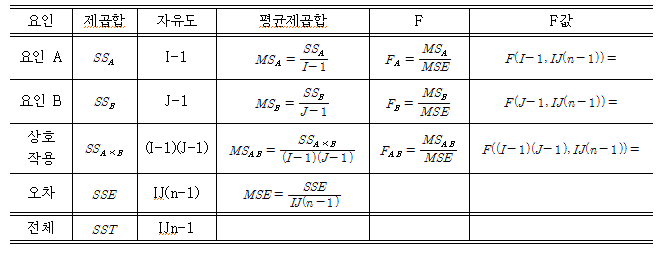
- SSa : 요인A 수준 평균값들 사이의 제곱합
- SSb : 요인B 수준 평균값들 사이의 제곱합
- I : 요인 A의 수준의 수
- J : 요인 B의 수준의 수
d. 가설설정
- H0
- A 변수에 따른 종속변수의 값에는 차이가 없다.
- B 변수에 따른 종속변수의 값에 차이가 없다. .
- A 와 B 변수의 상호작용 효과가 없다.
- H1 : Not H0
'3️⃣ Study at Univ > ○ 자격증 | 교육' 카테고리의 다른 글
| [빅분기] 3과목 빅데이터 모델링 : 2장 통계분석 기법_part2 (0) | 2022.03.31 |
|---|---|
| [빅분기] 3과목 빅데이터 모델링 : 2장 통계 분석기법 Part1 (0) | 2022.03.30 |
| [빅분기] 3과목 빅데이터 모델링 : 1장 분석모형설계 (0) | 2022.03.28 |
| [빅분기] 2과목 빅데이터 탐색 : 2장 데이터 탐색 (0) | 2022.03.26 |
| [빅분기] 2과목 빅데이터 탐색 : 1장 데이터 전처리 (0) | 2022.03.26 |
댓글