👀 계량경제학 개인 공부용 포스트 글입니다.
1. Treatment conditional on covariates
① Conditional Independence Assumption
◯ Motivation
• treatment effect 의 신뢰성을 어떻게 측정할까
▸ Cetris Paribus : all else being equal
▸ Treatment 는 treatment 와 control group 의 유일한 차이여야 한다. (다른 건 다 동일)
• treatment 가 모든 setting 에서 진짜로 random 할까
▸ observational study 뿐만 아니라, lab experiment 에서도 treatment 는 randomly 하게 할당되지 않을 수 있다.
▸public policy 혹은 firm strategy 는 eligibility condition 을 가지고 있는 것이 일반적이다.
※ Eligibility condition : 인과관계를 분석할 때, 그 관계가 어느 조건에서 유효한지를 판단하기 위한 기준이 되는 조건을 의미한다. 인과추론에서 자격조건 (ex. A와 B 사이에 다른 변수들의 영향은 없어야 한다) 을 설정하고 이를 충족시키는 것은 매우 중요하다.
• covariates Xi 에 대한 조건 (ex. holding the control variables fixed) 을 설정하여, treatment 의 randomness 를 만족시킬 수 있다.
• covariates (즉, CIA)에 대한 처리 조건의 무작위성은 여전히 하나의 가정에 해당한다. 공변량에 대한 조건화는 treatment 의 랜덤성을 확립하기 위한 시도이다.
◯ Conditional Independence Assumption
• Randomness of treatment is conditional on covariates

• Random treatment conditional on the covariates 는 고정된 공변량 (covariates) 을 알고 있다고 가정하기 때문에 selection-on-observables 라고 부른다.
• CIA 는 ignorability assumption, unconfoundedness assumption, exogenous treatment assumption 이라고 부른다.
② Subclassification
◯ Calculating treatment effect: Subclassification
• ATT 를 계산하는데 있어 CIA 의 역할

↪ Di 가 {Y1i, Y0i} 에 independent 하지 않기 때문이다.

↪ Xi 를 conditioning 하면 treatment effect 적용이 가능해진다.
↪ δx = E[Y1i | Xi, Di=1] - E[Y0i | Xi, Di=0] : simple mean difference between treated and control groups

↪ ATT 는 Xi | Di=1 의 가능한 값에 대한 δx 의 weighted average 를 통해 얻을 수 있다 ⇨ subclassification
◯ Subclassification example

• Xi = 0 일 때, δx 는 5-3 = 2 가 되고, Xi = 1 일 때, δx 는 8-4 = 4 가 된다.
• δ(ATT) = E[δx | Di=1] = 2/5*2 + 3/5*4 = 16/5 ⇨ weighted average
• δ(ATE) = E[δx] = 1/2*2 + 1/2*4 = 3
※ ATT : average treatment effect on the treated : 처치받은 그룹의 평균 처치효과로, 처치를 받은 그룹에 대한 평균적인 효과를 측정한다. 반면 ATE 는 Average Treatemtn Effect 로 전체 대상자 집단의 평균처치효과를 의미한다. ATE 는 처치받은 그룹과 처치를 받지 않은 그룹의 효과를 비교해 처치의 전반적인 효과를 파악한다.
③ Overlap Assumption
◯ Overlap assumption
• δ(ATT) 를 계산할 때, Overlap assumption 이 내포되어 있다.
• 0 < P(Di = 1 | Xi) < 1
• P(Di = 1 | Xi) 가 0이거나 1의 값을 가지면, 개별 유형의 처치효과에 관해, 데이터로부터 알 수 있는 것이 없다는걸 의미한다.
◯ Subclassification
• 필요한 가정 : CIA, Overlap

• 계산은 쉬우나, 차원의 저주에 빠질 수 있다. (결측데이터가 많은 경우)
• 다수의 Covariate 가 존재한다면, 셀의 숫자가 커야 한다.
2. Matching
① Exact matching
◯ [Recap] Regression
• 처치효과는 회귀분석을 사용하여 추정할 수도 있다. covariate 를 사용하여 아래와 같이 처치효과를 추정할 수 있다.
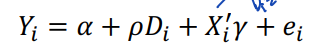
• CIA 는 E(ei | Di,Xi) = 0 을 의미하며, 이때의 ρ 는 처치의 인과효과를 추정한다.
◯ Motivation : Matching
• 회귀분석과 달리 matching 은 matching variable 과 selection bias 의 수학적인 형태를 가정하지 않는다.
• To make the control and treatment more similar in the observables
◯ Exact Matching
• Mathing 에선 (반대의 값을 가지는 Di 와 가장 근접한 값을 가지는 Xi) 로 구성된 unit 을 사용하여, missing 된 unit 의 potential outcome 을 대체 (impute) 한다.
• CIA 는 이러한 접근이 유효한 가장 중요한 이유 중 하나다. (Xi, Di) 에 대한 conditioning 은 random 한 것으로 간주될 수 있다. 따라서 같은 Xi 를 갖는다면, E[Y0i | Xi, Di=1] 은 E[Y0i | Xi, Di=0] 과 동일한 값을 가진다고 볼 수 있다.
• 따라서 각 unit 은 두 개의 potential outcome 에 대한 관측값을 가지게 된다 (둘 중 하나는 imputed 됨)
• Xi 측면에서 정확한 일치의 평균을 사용해 누락된 potential outcome 의 결과를 대체한다.
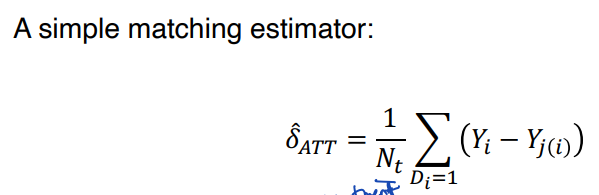
↪ Nt : # of treated units (처치받은 unit 의 개수)
↪ Yj(i) : outcome of the matched unit, j, for i
↪ Dj ≠ Di , Xj = Xi ⭐
• 만약 match 될 수 있는 unit 이 하나 이상이면 → 아래의 수식과 같이 정확하게 match 되는 unit 들 에 대한 Yi 의 평균을 취하여 사용한다.
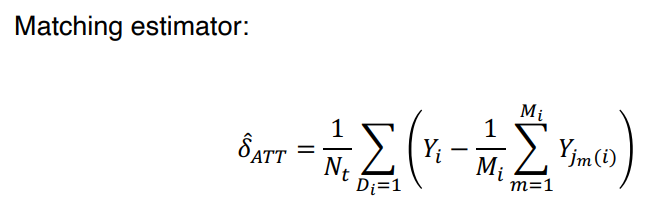
↪ Yjm(i) : the outcome of the m_th matched unit, jm, for i
↪ Mi : total # of matches for i
↪ Mi 는 2처럼 작은 숫자 범위로 간주한다. 만약 2보다 크다면, 그들 중에 랜덤하게 2개를 선택하는 방식을 취한다.
◯ Example
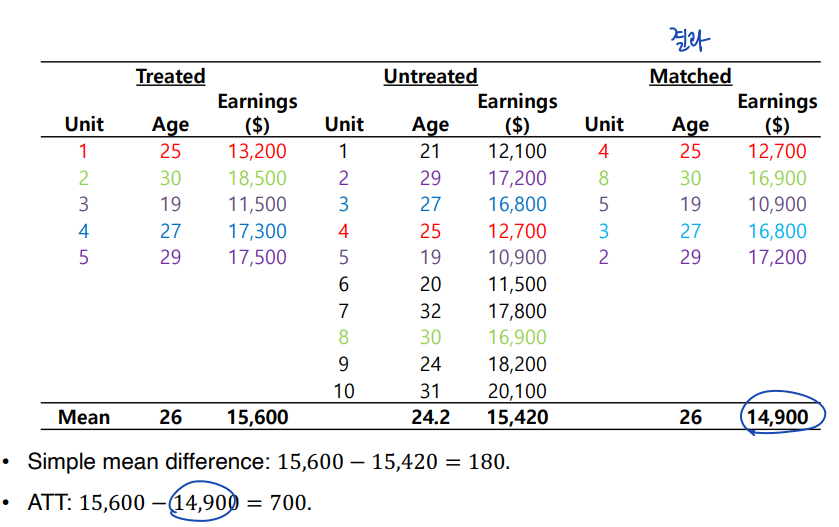
② Approximate matching (nearest neighbor, propensity scores)
◯ Approximate Matching
• 실제 세계에서는 정확하게 match 되는 경우는 거의 불가능하다. 특히 covariate 의 수가 매우 크다면 더욱 그러하다. 이런 경우에는 approximate matching 이 가능하다. 크게 Nearest neighbor matching 과 Propensity score matching 이 있다.
• Approximate matching 에선 missing potential outcome 을 대체하기 위해 가장 비슷한 값 (closest) 을 가지는 Xi 를 사용한다.
◯ Nearest neighbor matching , Measuring the Closeness in Xi
• nearest neighbor matching 에서는, covariates 를 매칭하기 위해, 거리 기반 함수들을 사용한다.
1. 유클리디안 거리
2. 정규화된 유클리디안 거리
3. 마할라노비스 거리
• 유클리디안 거리는, 변수의 scale 에 의존한다는 문제가 존재한다.
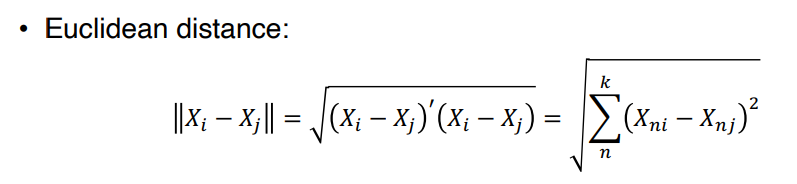
• 따라서 scale 을 조정한 정규화된 유클리디안 거리를 사용하기도 한다.

• 마할라노비스 거리
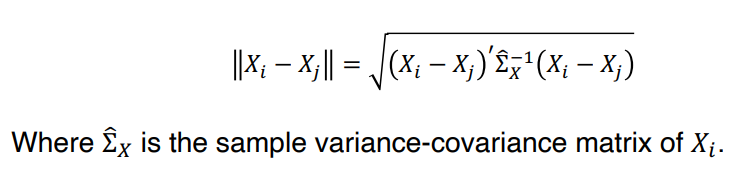
↪ scale dependence 를 없애며, covariate 사이의 상관관계를 고려한다.
↪ Example
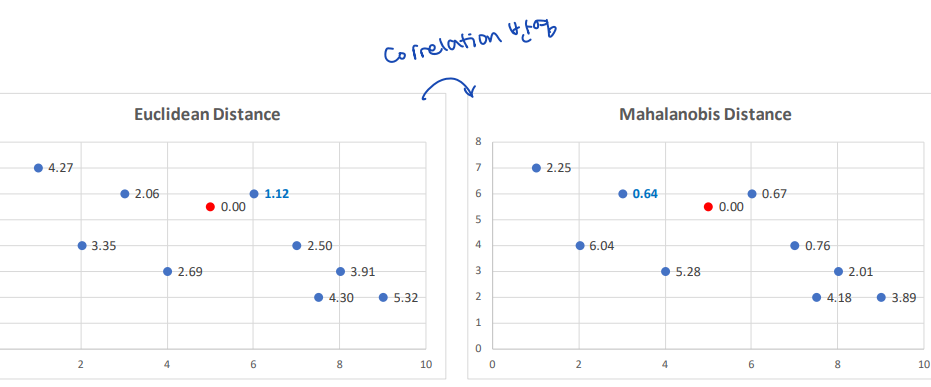
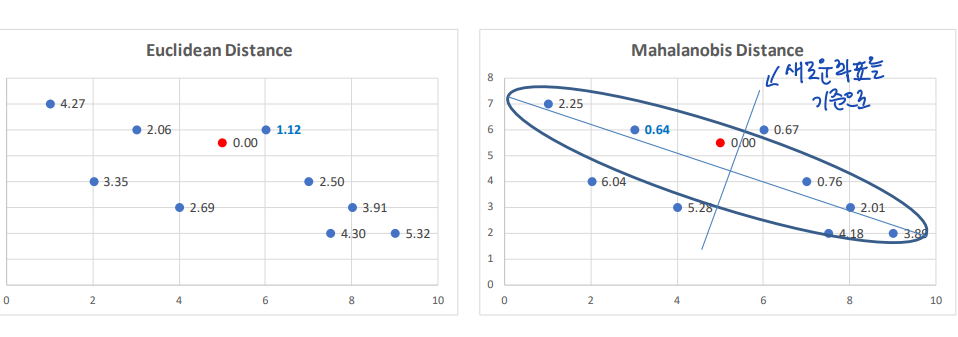
직관적으로 생각해보면, 마할라노비스 거리는 covariate 사이의 일반적인 trend 에서 멀리 벗어나 있는 데이터의 경우에는 penalty 를 부여하는 방식으로 동작한다.
③ Propensity Score Matching
◯ Propensity Score Matching
• Two steps
(1) logit 혹은 probit 같은 parametric model 을 사용하여 P(Xi) 를 추정한다.
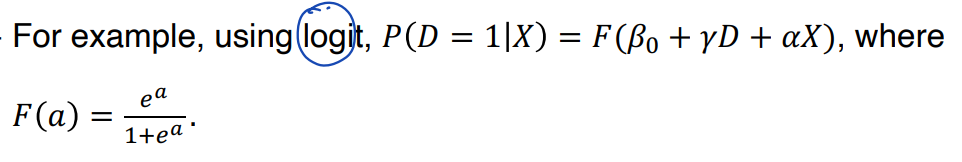
(2) 그리고 Direct PS matching 혹은 inverse probability weighting 을 사용하여 treatment effect 를 추정한다.
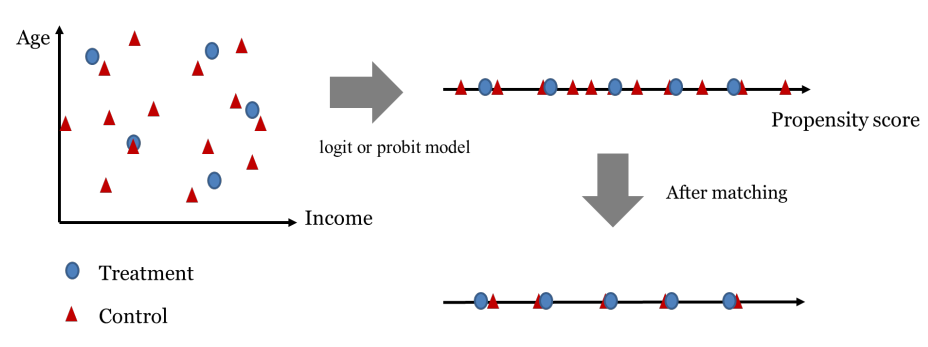
• Example : Direct PSM
◯ Inverse Probability Weighting
• IPW
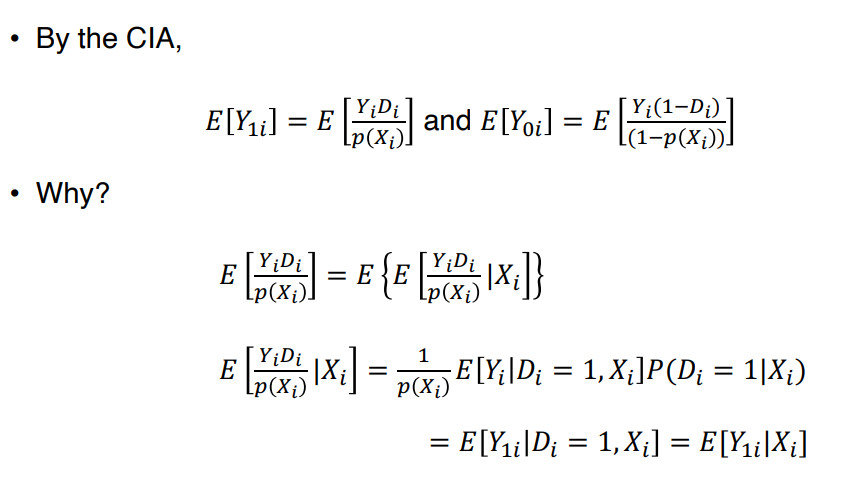

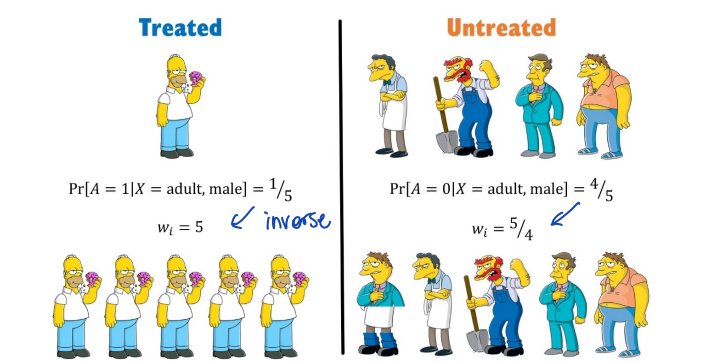
• Example
도넛을 먹은 (=treatment) 후 단 것에 대한 수요에 관심이 있다고 하자. 이때 treatment 는 1, control 은 4로 구성된 imbalanced panel 로 데이터가 구성되어 있다고 했을 때, 각 group 에서의 평균적인 demand 를 계산할 수 있을 것이고 이러한 차이가 treated 에 의해 발생했다고 말하기는 어려울 것이다. 오히려 남성은 도넛을 별로 먹지 않는다는 성별에 의해 이러한 차이가 일어난 것으로 볼 수 있다. IPW 의 아이디어는, 이러한 불균형한 panel 을 balanced 한 panel 로 만드는 것이다 (pseudo-population). 이렇게 되면, adult-male 에 대한 영향을 없앨 수 있고, treatment 에 대한 영향만 살펴볼 수 있다.
◯ Example
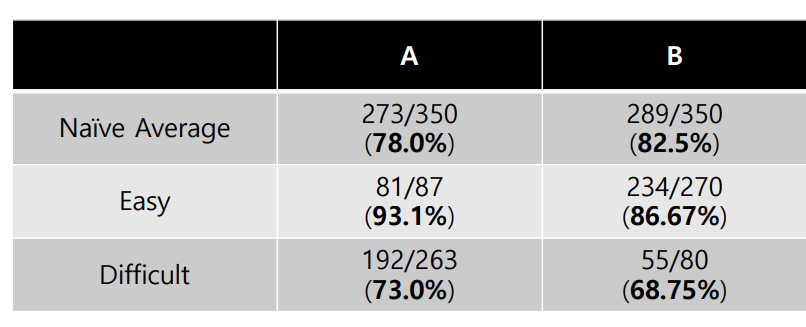
• Naive average 를 보면 B 가 전반적으로 더 좋은 success rate 을 가졌으나, Easy 와 Difficult 각각을 보면 A가 더 좋은 결과를 보인다. 이는 B가 Easy 에 대부분의 관측치가 쏠려있고, A는 Difficult 에 관측치가 쏠려있어서 심슨의 역설이 생긴 것이다.
④ Critiques of Matching
• CIA 가정에 대해 회의적으로 보는 사람들 때문에 Matching 은 경제학에서 더이상 인기있는 방법론이 아니다. 이들은 matching estimator 가 estimators 에 대해 항상 consistent 하고 robust 하진 않다고 주장한다.
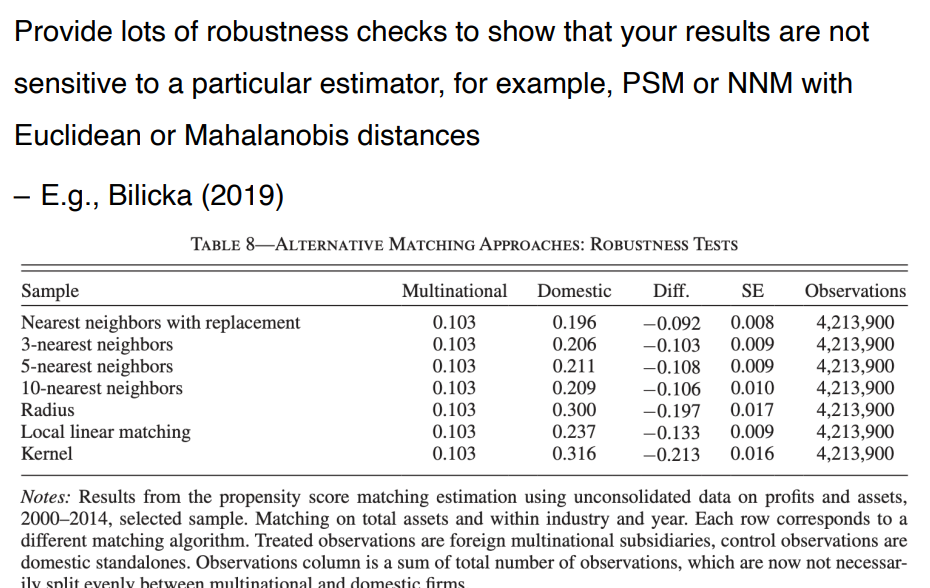
• matching 을 사용하는데 있어 매우 rigorous 하다. 어떻게 treatment 와 control group 을 match 했는지 매우 구체적으로 제시해주어야 하고, 결과가 특정 estimator 에 민감하지 않음을 보여주기 위해 많은 robustness check 을 진행해야 한다.

'1️⃣ AI•DS > ⚾ 계량경제•통계' 카테고리의 다른 글
| 계량경제학 강의_한치록_단순회귀 5장, 6장 (0) | 2023.05.13 |
|---|---|
| 계량경제학 강의_한치록_단순회귀 4장 (0) | 2023.05.12 |
| 계량경제학 강의_한치록_단순회귀 3장 (0) | 2023.05.11 |
| 계량경제학 강의_한치록_단순회귀 2.5~2.7장 (1) | 2023.05.10 |
| 계량경제학 스터디 Lecture 2. Regression (1) | 2023.05.10 |
댓글