1. Basic Concepts
① Definition
• Classification task
• Given a collection of records (training set), we find a model for the class attribute as a function of the values of other attributes. Each record contains a set of attributes, and one of the attributes is the class.
• Previously unseen records (test set) should be assigned a class as accurately as possible
↪ A test set is used to determine the accuracy of the model. Usually, the given data set is divided into training and test sets, with the training set used to build the model and the test set used to validate it
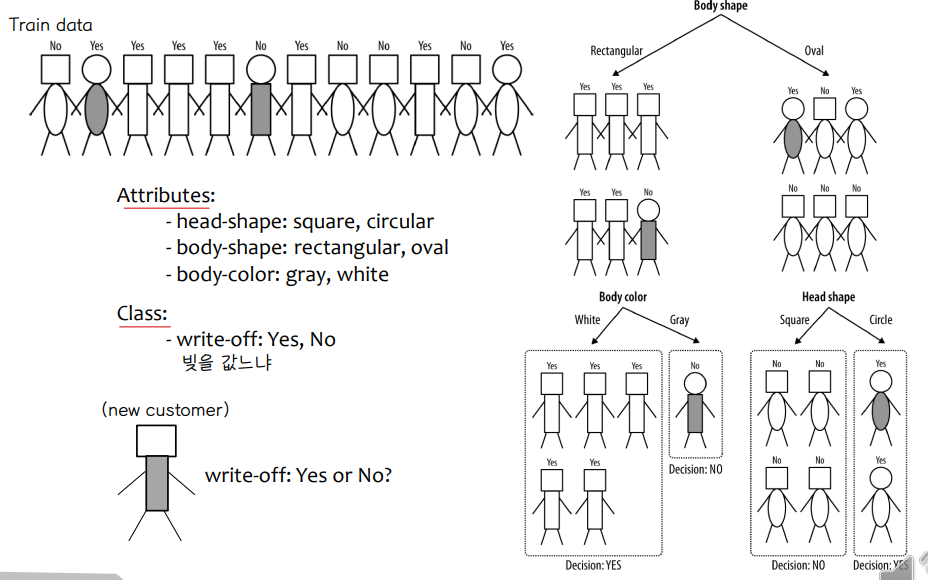
② Example
• Predicting tumor cells as benign or malignant (종양 양성음성)
• Classifying credit card transactions as legitimate or fraudulent (사기거래탐지)
• Classifying secondary structures of protein as alpha-helix, beta-sheet, or random coil
• Categorizing news stories as finance, weather, entertainment, sports, etc
③ techniques

2. Decision Tree Induction
① Example
• All the leaf node have a single same label
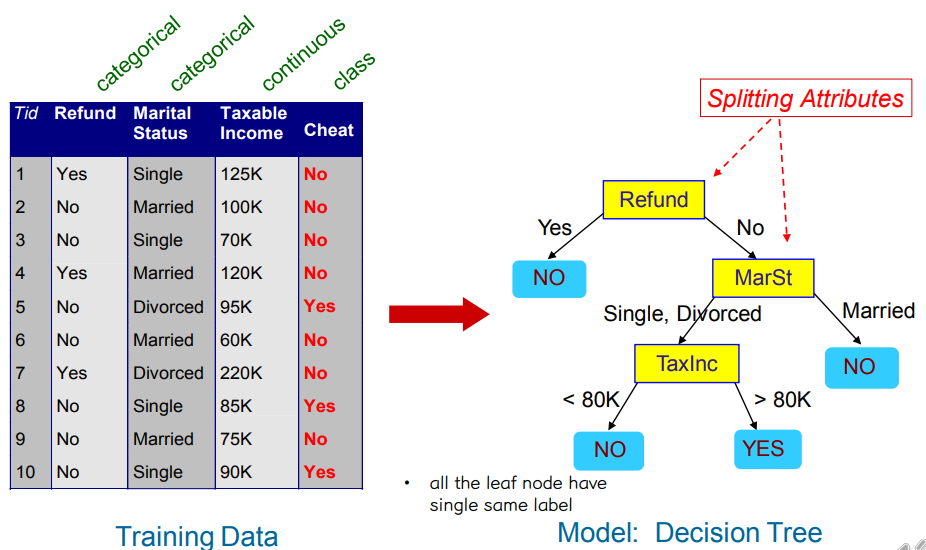
• There could be more than one tree that fits the same data
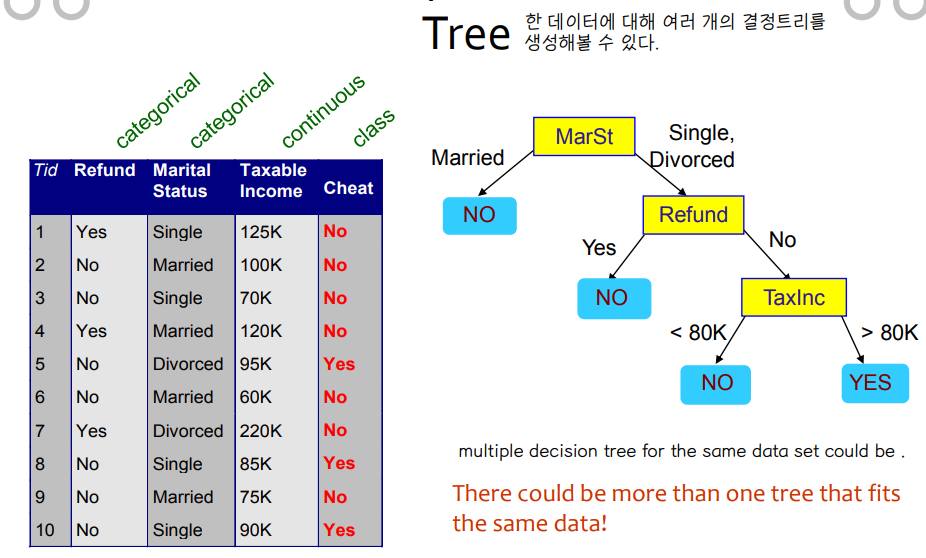
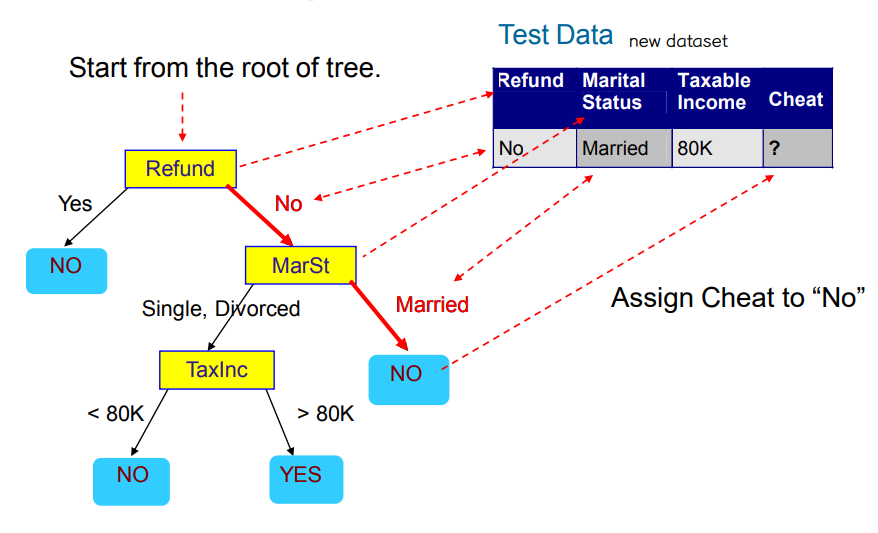
② Decision tree classification
• Train, test dataset
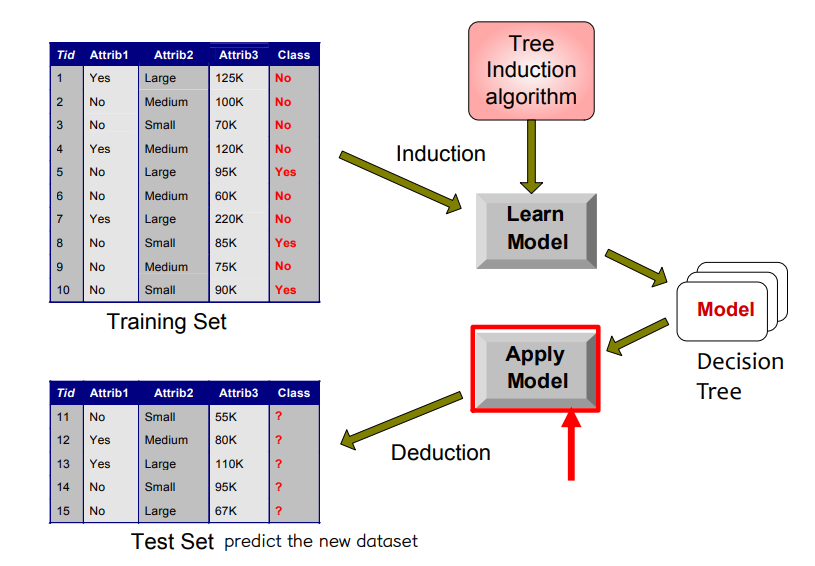
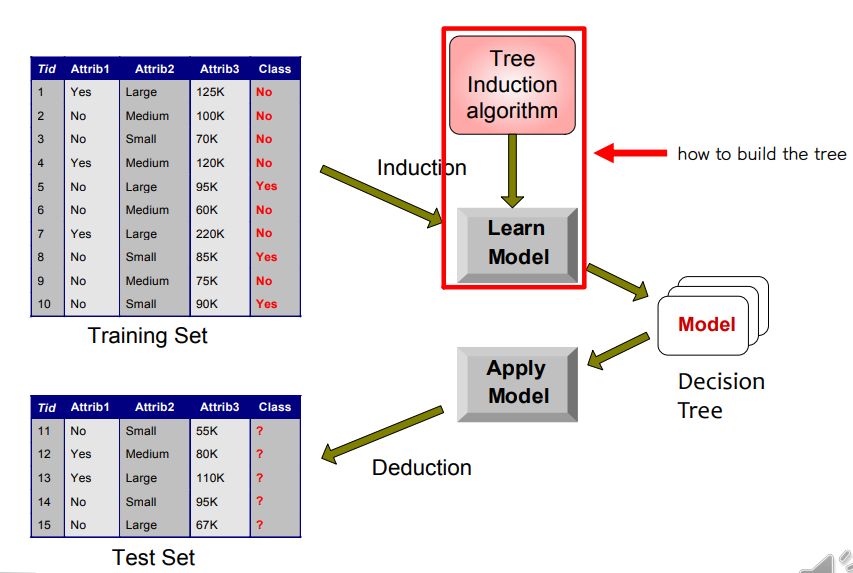
• Tree Induction: Greedy strategy
↪ Split the records based on an attribute test that optimizes certain criterion (gini index, gain ratio...)
↪ 데이터를 split 하는 방법
(1) attribute 에 대해 condition 을 어떻게 구체화 할까 (test 조건을 어떻게 설정할까)
(2) best split 을 어떻게 결정할까, 언제 split 을 멈출까
③ How to Specify Test Condition
• How to Specify Test Condition
↪ (1) Depend on attributes types : nominal, ordinal, continuous
↪ (2) Depends on number of ways to split : 2-way split, multi-way split
A. Splitting based on nominal attributes
↪ Multi-way split : use as many partitions as distinct values
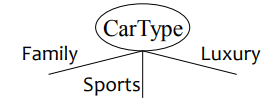
↪ Binary split: Divide values into two subsets, need to find optimal partitioning
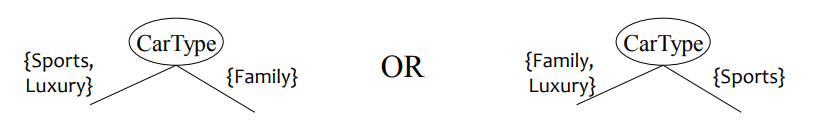
B. Splitting based on Ordinal attributes
↪ Multi-way split : Use as many partitions as distinct values
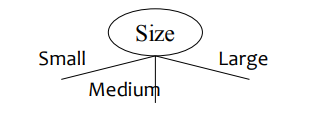
↪ Binary split: Divide values into two subsets; need to find optimal partitioning
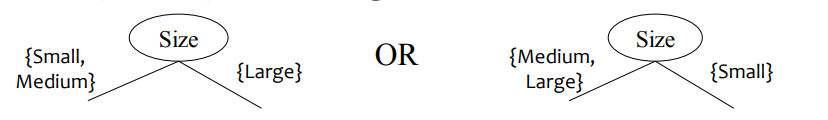
Ordinal attributes 에서 binary split 을 할 때, 아래와 같이 나누는 것은 적절하지 않다. {Small, Large} 는 consecutive 한 값이 아니기 때문이다. 각 branch 의 child node 는 의미있는 combination 이여야 한다.

C. Splitting based on Continuous attributes
Binary split 의 경우에는, 가장 분류를 잘 할 수 있는 best cut point 를 찾는 것이 중요하고, Multiway split 의 경우에는 discretization (이산화, 구간화) 를 잘 수행해야 한다.

④ How to Determine the Best Split
• How to Determine the Best Split
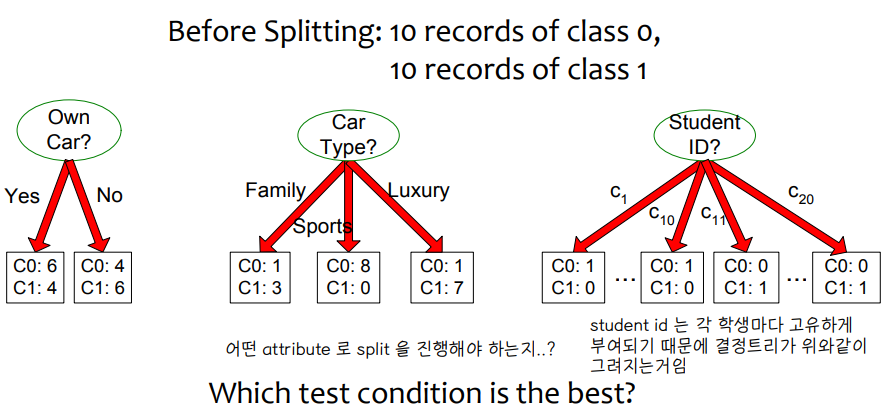
↪ 어떤 test condition 이 최선일까
↪ greedy 접근을 사용할 때, homogeneous class distribution 을 가진 노드를 기준으로 트리를 형성하는 것이 좋다.

↪ Non-Homogeneous = high degree of impurity
↪ Homogeneous = low degree of impurity
• Example
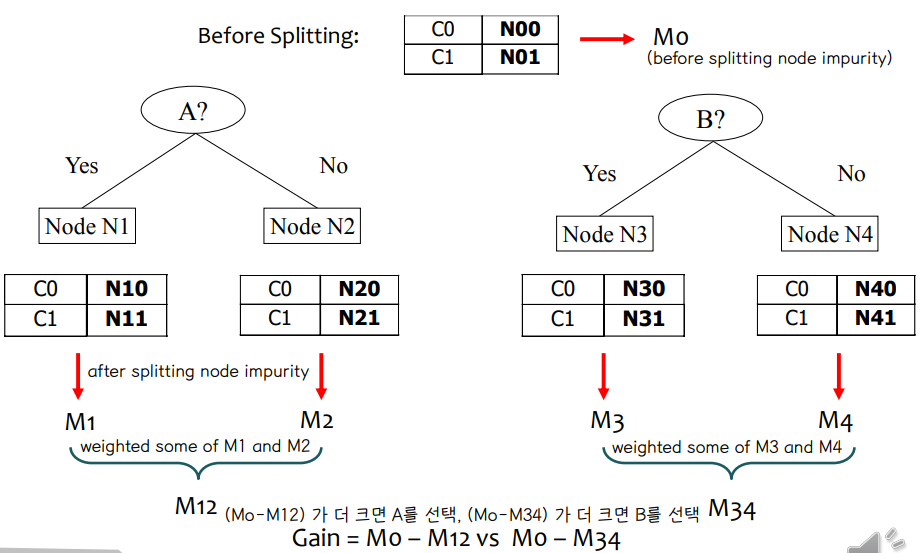
↪ M0 : split 전의 노드 불순도 , M12 : A 변수를 기준으로 split 한 후의 노드 불순도, M34 : B 변수를 기준으로 split 한 후의 노드 불순도
↪ Gain = M0 - M12 vs M0 - M34 ⇨ (M0-M12) 가 크면 A를 선택, (M0-M34) 가 더 크면 B를 선택
3. GINI Index (CART)
① Measure of Impurity : GINI
• 주어진 노드 t 에서 지니계수 구하기
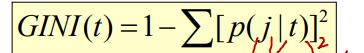
⇨ P(j | t) = 노드 t에서 class j 의 상대빈도
⇨ 지니계수의 값이 작을수록 좋다.
⇨ 지니계수 최댓값 = 1 - 1/nc , nc = # of records : 모든 records 가 모든 class 에 동등하게 분포되었을 때를 의미한다. 이때 interesting information 은 least 한 상태이다. (얻을 수 있는 정보가 없는 최악의 case). P(j | t) = 1/nc 라고 볼 수 있다.
⇨ 지니계수 최솟값 = 0.0 : 모든 recoreds 가 하나의 class 로만 할당된 상태를 의미한다. 이때 interesting information 은 most 한 상태이다. (얻을 수 있는 정보가 많은 case)
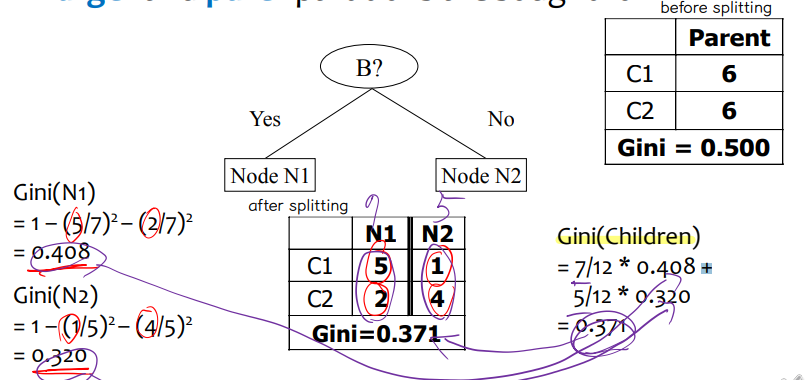
• Example

• 지니계수를 기준으로 split 하는 방법
↪ Used in CART (Classification and Regression Tree), SLIQ, SPRINT
↪ 노드 p 를 k 의 partition (children) 으로 쪼개고자 할 때, split 의 quality 를 측정하는 방법은 아래와 같다.

↪ child i 에서의 record 의 갯수를 ni, node p 에서의 record 의 갯수를 n 이라고 할 때, 각 child node 에 대해 지니계수를 계산하고 weighted sum 을 한다.
② Attributes
• Binary
↪ two partition 으로 분류
↪ Larger and purer partitions are sought for
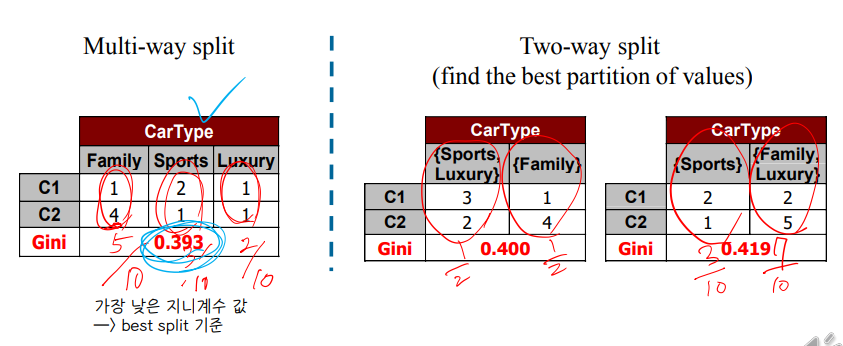
• Categorical
↪ For each distinct value, we gather counts for each class in the dataset and use the count matrix to make decisions
• Continuous
↪ Several choices for the splitting value v

↪ 가능한 splitting values 의 개수 = distinct values 의 개수

↪ 최선의 v 를 선택하는 방법 : 각 v 값에 대해 데이터베이스를 스캔한다. count matrix 를 설계하고 지니계수를 계산한다 → 그러나 일일히 계산하는 것은 계산적으로 비효율적이다.
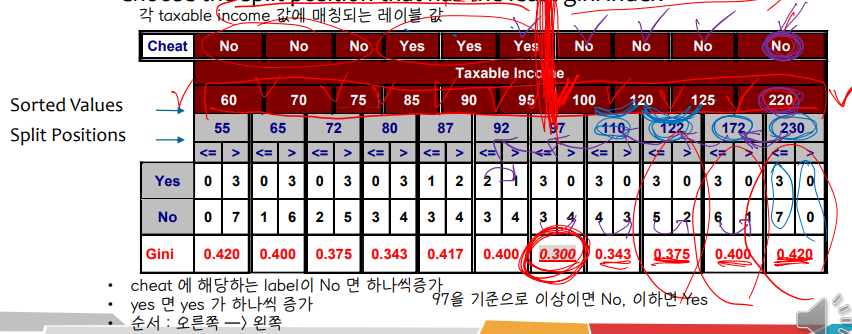
↪ 효율적으로 계산하는 방법 : 각 attribute 에 대해, value 를 정렬하고, 선형적으로 이 value 들을 스캔하여, 각 time 마다 count matrix 와 지니계수를 업데이트한다. 가장 최소의 지니계수 값을 가지는 위치를 기준으로 split 을 한다.
예를들어 처음 데이터프레임에서 Taxable income 변수는 continous 변수에 해당하므로 위의 방법처럼 best split position 을 찾아볼 수 있다. 일단 taxable income 변수 값들을 정렬한 후에, 각 값들의 중간 값을 split position 으로 잡는다. 해당 중간 값을 기준으로 초과, 이하로 split 을 잡은 후에, 각 split position 을 기준으로 지니계수를 계산한다. cheat 변수의 레이블을 기준으로 Yes, No 에 할당하는 경우의 수를 쉽게 계산해볼 수 있다. (직접 해보기)
③ Drawback of the Gini Index
• 지니계수의 한계점
A. Bias towards equally-sized subsets
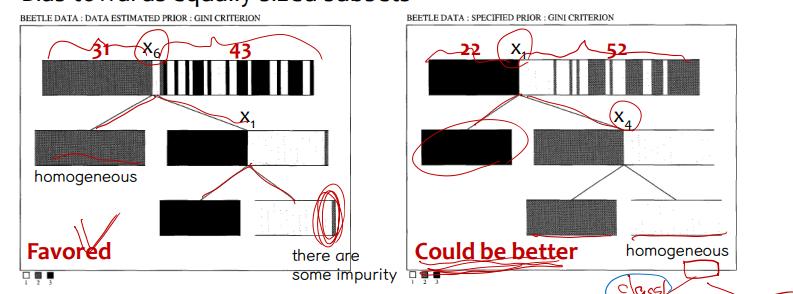
• greedy 한 방식으로 동작하기 때문에, 이후의 efficient 는 고려하지 않고, 해당 step 에서 가장 최선을 선택한다. 따라서 위의 그림에선 x6 이 좀 더 balance 되게 나뉘어저 왼쪽 분류를 최종적으로 선택하게 된다. 그러나 x1 이 이후 분류에서 좀 더 homogeneous 하게 (balance 되게) 나눠져 최종 불순도의 결과는 x1 이 더 좋다.
• pure offspring
총 7개의 class 가 존재할 때, class1 과 class2 에 의해 데이터셋이 나누어진다고 한다면
- option 1 : class1 과 2로 가능한 빨리 분리 ⇨ favored
- option 2 : (class1,2) 와 다른 class 들로 분리 ⇨ could be better : 최종적인 결과에서는 더 좋겠지만, class1 과 2가 섞여 있는 것은 pure 하지 않기 때문에 선호하진 않음
④ Algorithm CART
1. 각 attribute의 best split 을 찾는다 : 노드가 분리될 때 지니계수를 낮추는 point 가 best split point 이다.
2. node 의 best split 을 찾는다 : step1 에서 찾은 best split 값들 중에 지니 계수가 가장 낮은 것을 선택한다.
3. stopping rule 이 만족되지 않을 때까지 step2 를 반복한다.
'1️⃣ AI•DS > 📕 머신러닝' 카테고리의 다른 글
| Uplift modeling (0) | 2023.06.06 |
|---|---|
| 데이터마이닝 Association analysis (0) | 2023.03.29 |
| 데이터마이닝 Preprocessing ③ (0) | 2023.03.29 |
| 데이터마이닝 Preprocessing ② (0) | 2023.03.15 |
| 데이터마이닝 Preprocessing ① (1) | 2023.03.15 |




댓글